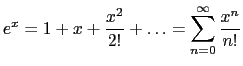Licence de Physique -- Premier partiel d'optique
Durée 2 h
Date: Documents autorisés : formulaire de TF +
1 feuille A4 manuscrite recto-verso
Les questions 1, 2, 3 et 4 sont indépendantes
On considère une fente de longueur 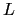 dans la direction
dans la direction 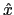 et de largeur très très faible dans la direction
et de largeur très très faible dans la direction 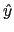 . A cette fente est accolée un film plastique de manière à ce que le
coefficient de transmission de l'ensemble s'écrive
. A cette fente est accolée un film plastique de manière à ce que le
coefficient de transmission de l'ensemble s'écrive
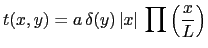
avec 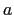 un nombre réel positif. Ce masque, placé dans
le plan
un nombre réel positif. Ce masque, placé dans
le plan 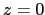 est éclairé par une onde plane de longueur
d'onde
est éclairé par une onde plane de longueur
d'onde 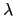 et d'amplitude
et d'amplitude 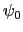 . On se place dans les conditions de Gauss.
. On se place dans les conditions de Gauss.
- Quelle doit être la dimension de
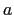 (quelle unité) et
pourquoi ?
(quelle unité) et
pourquoi ?
- Question de cours : on se place en un point de coordonnées
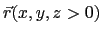 ; pour quelles valeurs de
; pour quelles valeurs de 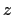 peut-on faire
l'approximation du champ lointain (diffraction à l'infini de
Fraunhöffer). On ne demande pas de démonstration.
peut-on faire
l'approximation du champ lointain (diffraction à l'infini de
Fraunhöffer). On ne demande pas de démonstration.
- Diffraction à l'infini
- Tracer
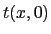 (sans prendre en compte le
(sans prendre en compte le 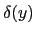 ).
).
- En introduisant une fonction triangle, réécrire l'expression
de
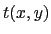 (on rappelle que le produit d'une porte de
largeur
(on rappelle que le produit d'une porte de
largeur 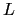 par une fonction
par une fonction 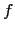 de
largeur inférieure ou égale à
de
largeur inférieure ou égale à 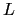 vaut
vaut 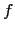 )
)
- En déduire l'amplitude
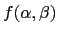 diffractée à l'infini dans une direction
diffractée à l'infini dans une direction 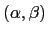 .
.
- Tracez l'allure du graphe de
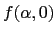 (faire apparaitre les valeurs ou
(faire apparaitre les valeurs ou 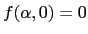 ).
).
- Diffraction de Fresnel : on se place maintenant à une distance
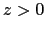 du masque, on est dans le domaine du champ proche
(diffraction de Fresnel). On se place sur l'axe optique
du masque, on est dans le domaine du champ proche
(diffraction de Fresnel). On se place sur l'axe optique 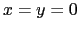 .
.
- Ecrire sous forme d'une intégrale l'expression de l'amplitude
en
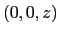 (on la notera
(on la notera 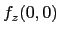 ).
).
- Faire le calcul de l'intégrale (on rappelle que la dérivée de
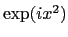 est
est 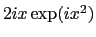 )
)
- En déduire l'intensité sur
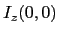 sur l'axe et montrer qu'elle s'annule pour certaines valeurs de
sur l'axe et montrer qu'elle s'annule pour certaines valeurs de 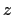 .
.
On considère une lame de verre d'indice 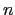 taillée en forme de
``tôle ondulée''. Son épaisseur s'écrit
taillée en forme de
``tôle ondulée''. Son épaisseur s'écrit 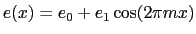 . Cette lame est éclairée sous incidence normale par une onde plane
d'amplitude incidente
. Cette lame est éclairée sous incidence normale par une onde plane
d'amplitude incidente 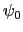 dans le plan de la
lame. La longueur d'onde est notée
dans le plan de la
lame. La longueur d'onde est notée 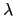 . On fait l'hypothèse
. On fait l'hypothèse 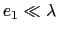 .
.
- Ecrire le coefficient de transmission de la lame. Par un
développement limité au premier ordre montrer que l'intensité
diffractée à l'infini (dans une direction
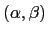 ) est composée de 3 termes (ordres 0 et
) est composée de 3 termes (ordres 0 et 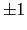 ).
).
- On augmente la valeur de
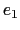 de sorte que le
développement limité de la question précédente doit maintenant se faire
au second ordre.
de sorte que le
développement limité de la question précédente doit maintenant se faire
au second ordre.
- Ecrire, dans cette approximation, le coefficient de
transmission de la lame
- Calculer l'intensité diffractée à l'infini (dans une
direction
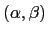 ) et tracer son graphe
) et tracer son graphe
- Quelles différences y-a-il avec la question 1 ?
- Calculer le rapport d'intensité entre l'ordre 2 et l'ordre 0.
On le notera
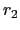
- On suppose que l'on peut négliger le second ordre si
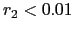 . A quelles valeurs de
. A quelles valeurs de 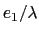 celà correspond-il ? (on prendra
celà correspond-il ? (on prendra 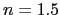 ).
).
- Généralisation à
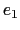 quelconque : en utilisant le
développement en série de l'exponentielle donné ci-dessous, expliquer
pourquoi l'intensité diffractée à l'infini présente des pics dans tous
les ordres
quelconque : en utilisant le
développement en série de l'exponentielle donné ci-dessous, expliquer
pourquoi l'intensité diffractée à l'infini présente des pics dans tous
les ordres 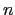 (on ne demande pas un calcul explicite de
l'amplitude diffractée).
(on ne demande pas un calcul explicite de
l'amplitude diffractée).
- Question indépendante des précédentes : Rappeler
pourquoi il existe un ordre maximal observable, et donner sa valeur si
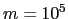 m
m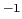 et
et 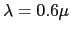 m.
m.
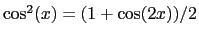

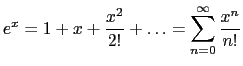
Voir la solution
![]() dans la direction
dans la direction ![]() et de largeur très très faible dans la direction
et de largeur très très faible dans la direction ![]() . A cette fente est accolée un film plastique de manière à ce que le
coefficient de transmission de l'ensemble s'écrive
. A cette fente est accolée un film plastique de manière à ce que le
coefficient de transmission de l'ensemble s'écrive