L3 Physique -- Premier partiel d'optique
19 Octobre 2010
Date: Durée 2h
Documents autorisés : 1 feuille A4 manuscrite RV + formulaire de TF
Les deux exercices sont indépendants.
L'interféromètre de Mach-Zehnder est schématisé sur la figure ci-dessous. Il fait partie de la même famille que celui de Michelson étudié en TD (les interféromètres à division d'amplitude) mais propose deux sorties (deux plans d'observation des interférences) au lieu d'une seule. Il est constitué de 2 miroirs 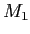 et
et 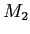 et de 2 lames séparatrices
et de 2 lames séparatrices 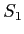 et
et 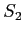 . Ces séparatrices sont des lames à faces parallèles dont une face est réfléchissante et l'autre non (traitement anti-reflet). Elles n'ont pas le même coefficient de réflexion selon qu'elles sont éclairées par l'avant ou l'arrière.
. Ces séparatrices sont des lames à faces parallèles dont une face est réfléchissante et l'autre non (traitement anti-reflet). Elles n'ont pas le même coefficient de réflexion selon qu'elles sont éclairées par l'avant ou l'arrière.
![\includegraphics[width=10cm]{mz.eps}](img44.png)
L'onde incidente est séparée en deux ondes secondaires au passage de 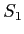 . L'onde secondaire 1 emprunte le trajet 1 : elle se réfléchit sur
. L'onde secondaire 1 emprunte le trajet 1 : elle se réfléchit sur 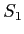 (plus précisément sur sa face avant), se réfléchit sur
(plus précisément sur sa face avant), se réfléchit sur 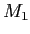 avant d'atteindre
avant d'atteindre 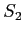 . Elle se sépare à nouveau en deux : une partie passe à travers
. Elle se sépare à nouveau en deux : une partie passe à travers 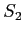 pour atteindre l'écran
pour atteindre l'écran 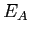 (sortie A de l'interféromètre), l'autre partie se réfléchit sur
(sortie A de l'interféromètre), l'autre partie se réfléchit sur 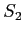 (face arrière) pour atteindre l'écran
(face arrière) pour atteindre l'écran 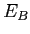 (sortie B de l'interféromètre).
(sortie B de l'interféromètre).
L'onde secondaire 2 passe à travers 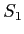 , puis sur
, puis sur 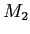 et se sépare encore en deux au niveau de
et se sépare encore en deux au niveau de 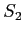 : une partie passe à travers
: une partie passe à travers 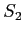 pour atteindre
pour atteindre 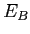 , l'autre se réfléchit sur
, l'autre se réfléchit sur 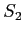 (face avant) pour atteindre
(face avant) pour atteindre 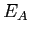 . On note
. On note 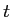 le coefficient de transmission en amplitude des séparatrices (identique pour
le coefficient de transmission en amplitude des séparatrices (identique pour 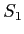 et
et 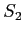 ),
), 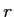 le coefficient de réflexion (en amplitude) de la face avant des séparatrices,
le coefficient de réflexion (en amplitude) de la face avant des séparatrices, 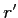 le coefficient de réflexion de leur face arrière. On a
le coefficient de réflexion de leur face arrière. On a
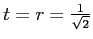 et
et
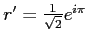 .
.
Les 4 trajets possibles sont résumés ci-dessous :
- Le trajet
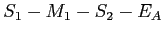 : onde
: onde 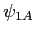 . Elle a subi une réflexion (coefficient de réflexion
. Elle a subi une réflexion (coefficient de réflexion 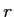 ) puis une transmission (coefficient de transmission
) puis une transmission (coefficient de transmission 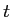 )
)
- Le trajet
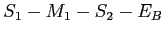 : onde
: onde 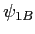 (réflexion
(réflexion 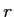 puis réflexion
puis réflexion 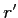 )
)
- Le trajet
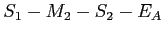 : onde
: onde 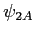 (transmission
(transmission 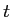 puis réflexion
puis réflexion 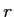 )
)
- Le trajet
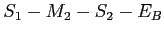 : onde
: onde 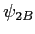 (transmission
(transmission 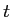 puis transmission
puis transmission 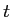 )
)
L'onde incidente est plane et monochromatique de longueur d'onde 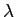 . Elle se propage parallèlement à l'axe
. Elle se propage parallèlement à l'axe 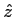 (dans la direction des
(dans la direction des 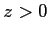 ) et son amplitude complexe est
) et son amplitude complexe est 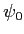 dans le plan
dans le plan 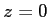 . On appelle
. On appelle 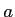 la distance
la distance 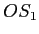 ,
, 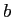 la distance
la distance
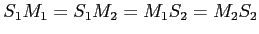 , et
, et 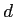 la distance
la distance
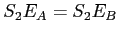 . On note
. On note 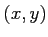 les coordonnées d'un point dans le plan
les coordonnées d'un point dans le plan 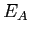 ou
ou 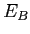 .
.
- Ecrire l'amplitude complexe de
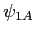 et
et 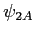 . En déduire l'intensité
. En déduire l'intensité 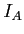 dans le plan
dans le plan 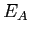
- Ecrire l'amplitude complexe de
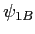 et
et 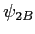 . En déduire l'intensité
. En déduire l'intensité 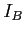 dans le plan
dans le plan 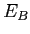
- Y-a-t-il conservation de la puissance lumineuse entre le plan
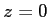 et les deux sorties de l'interféromètre (répondez en quelques lignes) ?
et les deux sorties de l'interféromètre (répondez en quelques lignes) ?
- On introduit dans le trajet 1 une petite lame à faces parallèles d'indice
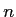 et d'épaisseur
et d'épaisseur 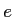
- Ecrire le coefficient de transmission de la lame
- Réécrire les amplitudes complexes de
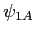 et
et 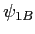 en tenant compte de la lame
en tenant compte de la lame
- Calculer les intensités
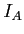 et
et 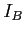 sur les deux écrans. La puissance lumineuse est-elle toujours conservée ?
sur les deux écrans. La puissance lumineuse est-elle toujours conservée ?
- Quelles valeurs de
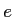 donnent un éclairage identique sur les deux écrans (
donnent un éclairage identique sur les deux écrans (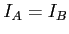 ) ?
) ?
- Pour quelles valeurs de
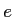 a-t-on
a-t-on
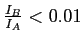 ? A.N. :
? A.N. : 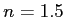 ,
,
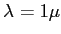 m. On rappelle que
m. On rappelle que
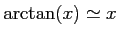 pour
pour 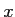 faible (le terme suivant est
faible (le terme suivant est 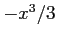 )
)
- Cet interféromètre vous semble-t-il assez sensible pour faire la mesure de faibles épaisseurs (de l'ordre de
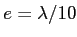 ), et pourquoi ?
), et pourquoi ?
*
On considère, dans le plan 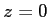 , un masque de coefficient de transmission
, un masque de coefficient de transmission
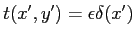 (indépendant de
(indépendant de 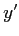 ) avec
) avec 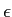 réel positif et
réel positif et 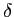 la distribution de Dirac. Cet écran, placé dans le plan
la distribution de Dirac. Cet écran, placé dans le plan 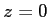 , est éclairé sous incidence normale par une onde plane d'amplitude
, est éclairé sous incidence normale par une onde plane d'amplitude 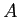 dans le plan du masque, se propageant vers les
dans le plan du masque, se propageant vers les 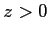 . la longueur d'onde est
. la longueur d'onde est 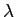 . On se place dans les conditions de l'optique paraxiale.
. On se place dans les conditions de l'optique paraxiale.
- Pourquoi parle-t-on de ``filament lumineux'' (c'est le titre de cet exercice) ? répondez en quelques phrases (on pourra considérer l'intensité à la sortie du masque).
- Quelle est la dimension (unité) de
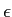 (et pourquoi) ?
(et pourquoi) ?
- Ecrire l'amplitude complexe
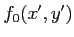 en
en 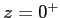 .
.
- Ecrire l'amplitude complexe
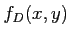 pour
pour 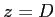 sous forme d'une convolution (principe de Huyghens-Fresnel)
sous forme d'une convolution (principe de Huyghens-Fresnel)
- Calculer
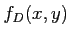
- De quelle variable ne dépend pas
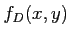 ? Quel est ce type d'onde ?
? Quel est ce type d'onde ?
- Ecrire la phase
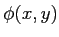 de l'onde.
de l'onde.
- Calculer l'intensité
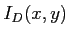 .
.
On réalise maintenant un dispositif dans lequel on mélange la lumière provenant du masque avec celle d'une onde plane sous incidence normale d'amplitude
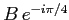 dans le plan
dans le plan 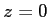 (même longueur d'onde).
(même longueur d'onde).
- Ecrire, dans le plan
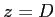 , l'amplitude complexe résultant de l'interférence de cette onde plane avec
, l'amplitude complexe résultant de l'interférence de cette onde plane avec  .
.
- Calculer l'intensité correspondante dans le cas où
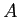 et
et 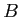 sont réels et
sont réels et
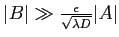
- Donner la position des maxima et minima d'intensité.
- Calculer le contraste de
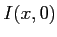
- Tracer l'allure du graphe de l'intensité
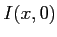 en fonction de
en fonction de 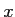 .
.
- Montrer que cette technique permet d'obtenir (éventuellement à une constante près) la phase
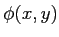 de l'onde
de l'onde  (elle est appelée ``holographie'', l'image dans le plan
(elle est appelée ``holographie'', l'image dans le plan 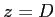 est un hologramme)
est un hologramme)
- On veut réaliser cette expérience à l'aide d'un interféromètre à division d'amplitude (de type Michelson ou Mach-Zehnder). Proposer un montage optique pour la réaliser.
Voir la solution
![\includegraphics[width=10cm]{mz.eps}](img44.png)
![\includegraphics[width=10cm]{mz.eps}](img44.png)
![]() . L'onde secondaire 1 emprunte le trajet 1 : elle se réfléchit sur
. L'onde secondaire 1 emprunte le trajet 1 : elle se réfléchit sur ![]() (plus précisément sur sa face avant), se réfléchit sur
(plus précisément sur sa face avant), se réfléchit sur ![]() avant d'atteindre
avant d'atteindre ![]() . Elle se sépare à nouveau en deux : une partie passe à travers
. Elle se sépare à nouveau en deux : une partie passe à travers ![]() pour atteindre l'écran
pour atteindre l'écran ![]() (sortie A de l'interféromètre), l'autre partie se réfléchit sur
(sortie A de l'interféromètre), l'autre partie se réfléchit sur ![]() (face arrière) pour atteindre l'écran
(face arrière) pour atteindre l'écran ![]() (sortie B de l'interféromètre).
(sortie B de l'interféromètre).
![]() , puis sur
, puis sur ![]() et se sépare encore en deux au niveau de
et se sépare encore en deux au niveau de ![]() : une partie passe à travers
: une partie passe à travers ![]() pour atteindre
pour atteindre ![]() , l'autre se réfléchit sur
, l'autre se réfléchit sur ![]() (face avant) pour atteindre
(face avant) pour atteindre ![]() . On note
. On note ![]() le coefficient de transmission en amplitude des séparatrices (identique pour
le coefficient de transmission en amplitude des séparatrices (identique pour ![]() et
et ![]() ),
), ![]() le coefficient de réflexion (en amplitude) de la face avant des séparatrices,
le coefficient de réflexion (en amplitude) de la face avant des séparatrices, ![]() le coefficient de réflexion de leur face arrière. On a
le coefficient de réflexion de leur face arrière. On a
![]() et
et
![]() .
.
![]() . Elle se propage parallèlement à l'axe
. Elle se propage parallèlement à l'axe ![]() (dans la direction des
(dans la direction des ![]() ) et son amplitude complexe est
) et son amplitude complexe est ![]() dans le plan
dans le plan ![]() . On appelle
. On appelle ![]() la distance
la distance ![]() ,
, ![]() la distance
la distance
![]() , et
, et ![]() la distance
la distance
![]() . On note
. On note ![]() les coordonnées d'un point dans le plan
les coordonnées d'un point dans le plan ![]() ou
ou ![]() .
.
![]() dans le plan
dans le plan ![]() (même longueur d'onde).
(même longueur d'onde).
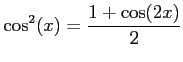

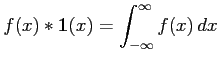
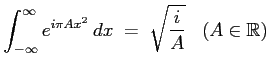
![$\displaystyle {\cal F}_u \left[e^{i\pi A x^2} \right] \; = \; \sqrt{\frac i A} \: \exp\left({-\frac{i\pi u^2} A}\right)\;\;\; (A\in\mathbb{R})
$](img70.gif)