Licence de Physique LP2b -- Electromagnétisme et optique
Session de Septembre 2000
Partie II -- Optique
Le laser Lune situé sur le plateau de Calern, non loin de Grasse, permet la mesure de la distance Terre-Lune au centimètre près. Le principe est la mesure du temps aller-retour d'un faisceau de lumière laser émis depuis un télescope d'un mètre cinquante de diamètre. Sur la Lune, des réflecteurs déposés par les astronautes lors des missions Apollo permettent de renvoyer une partie du faiseau vers la Terre. Connaissant la vitesse de la lumière, le temps de trajet aller-retour donne la distance Terre-Lune (en fait la distance entre le télescope et le réflecteur posé sur la Lune). Le but du problème proposé est d'étudier le rendement photométrique d'une version très simplifiée du Laser-Lune.
Le faisceau sortant du télescope peut être assimilé à une onde plane cohérente et monochromatique de longueur d'onde 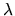 et d'amplitude
et d'amplitude 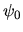 ayant traversé une ouverture circulaire de diamètre d. Cette onde se propage sur une distance D pour atteindre la Lune.
ayant traversé une ouverture circulaire de diamètre d. Cette onde se propage sur une distance D pour atteindre la Lune.
- 1.
- Question indépendante des suivantes : Ecrire, sous les conditions de l'optique paraxiale, la diffraction de Fresnel de l'onde sur la distance D. Quel développement limité fait-on dans l'approximation de Fraunhöffer (D très très grand, diffraction à l'infini) ? A quelle condition sur D, d et
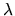 on peut considérer qu'il y a diffraction à l'infini . A.N.: d=1.5 m, D=384000 km,
on peut considérer qu'il y a diffraction à l'infini . A.N.: d=1.5 m, D=384000 km,
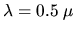 m. Cette approximation vous semble-elle justifiée ici ? Quelle est l'erreur commise sur l'amplitude complexe si l'on utilise cette approximation ?
m. Cette approximation vous semble-elle justifiée ici ? Quelle est l'erreur commise sur l'amplitude complexe si l'on utilise cette approximation ?
- 2.
- Soit W la puissance émise au sol (puissance lumineuse que transporte l'onde plane à la sortie du télescope de diamètre d), relier
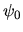 et W (on reliera d'abord W à l'intensité de l'onde).
et W (on reliera d'abord W à l'intensité de l'onde).
- 3.
- On suppose dans la suite que la Lune est suffisamment loin pour faire l'approximation de Frauhöffer. Etablir l'expression de l'amplitude diffractée à l'infini par une ouverture circulaire. On rappelle que la transformée de Fourier de
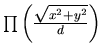 est
est
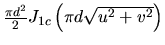 .
.
- 4.
- Quel est sur la Lune le diamètre
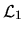 du premier anneau noir de la tache de diffraction ? A.N.: d=1.5 m, D=384000 km,
du premier anneau noir de la tache de diffraction ? A.N.: d=1.5 m, D=384000 km,
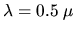 m.
m.
- 5.
- Donner l'expression de l'intensité I0 au centre de la figure de diffraction. Exprimer I0 en fonction de W (calculé question 2). On rappelle que
J1c(0)=0.5.
- 6.
- Le réflecteur sur la lune sera considéré pour l'exercice comme un miroir circulaire de diamètre a (en réalité il s'agit d'un coin de cube, mais celà ne change pas les ordres de grandeur). La condition
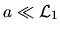 permet de considérer l'onde incidente comme plane sur la surface du réflecteur. Tout se passe donc comme si le miroir de diamètre a était éclairé sous incidence normale par une onde plane d'amplitude
permet de considérer l'onde incidente comme plane sur la surface du réflecteur. Tout se passe donc comme si le miroir de diamètre a était éclairé sous incidence normale par une onde plane d'amplitude 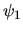 .
Ecrire l'expression de
.
Ecrire l'expression de 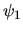 (on suppose que le réflecteur se trouve au centre de la tache de diffraction de l'onde incidente). Donner l'expression de la puissance lumineuse W1 réfléchie par le miroir et calculer numériquement le rapport W1/W pour a=10 cm.
(on suppose que le réflecteur se trouve au centre de la tache de diffraction de l'onde incidente). Donner l'expression de la puissance lumineuse W1 réfléchie par le miroir et calculer numériquement le rapport W1/W pour a=10 cm.
- 7.
- L'onde réfléchie se propage à nouveau sur la distance D pour revenir sur Terre. Quelle est la taille de la tache de diffraction
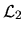 sur la Terre (diamètre du permier anneau noir) ? Calculez numériquement sa valeur. Quelle est l'intensité de l'onde au centre de la tache de diffraction ?
sur la Terre (diamètre du permier anneau noir) ? Calculez numériquement sa valeur. Quelle est l'intensité de l'onde au centre de la tache de diffraction ?
- 8.
- En considérant que
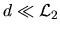 ,
donner la puissance W2 collectée par un télescope identique à celui qui a servi pour l'émission de l'onde incidente (diamètre d), observant l'onde retour et placé au centre de la tache de diffraction. Que pensez-vous du rendement (rapport W2/W) du Laser-Lune ?
,
donner la puissance W2 collectée par un télescope identique à celui qui a servi pour l'émission de l'onde incidente (diamètre d), observant l'onde retour et placé au centre de la tache de diffraction. Que pensez-vous du rendement (rapport W2/W) du Laser-Lune ?
- 9.
- La partie centrale de l'onde réfléchie est en fait captée par le télescope qui a servi à l'émission. Celui-ci fonctionne en mode pulsé : il émet pendant un temps
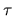 =400 picosecondes, puis passe en mode réception pendant environ 100 millisecondes, puis réémet pendant 400 picosecondes, et ainsi de suite, le tout pendant une dizaine de secondes. Soit Ei l'énergie lumineuse émise par le laser pendant le temps
=400 picosecondes, puis passe en mode réception pendant environ 100 millisecondes, puis réémet pendant 400 picosecondes, et ainsi de suite, le tout pendant une dizaine de secondes. Soit Ei l'énergie lumineuse émise par le laser pendant le temps 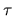 (un tir). Sachant que l'énergie que transporte un photon à la fréquence
(un tir). Sachant que l'énergie que transporte un photon à la fréquence 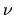 est
est 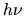 ,
calculer le nombre de photons émis par tir. A.N : Ei=400 mJ,
,
calculer le nombre de photons émis par tir. A.N : Ei=400 mJ,
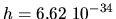 Js.
Js.
- 10.
- En utilisant le rendement calculé question 8, déduire le nombre de photons reçus en mode réception.
- 11.
- En réalité, le faisceau incident est perturbé par l'atmosphère terrestre qui a grosso-modo pour effet d'étendre la taille de la tache de diffraction sur la Lune à celle qu'aurait produite un télescope de diamètre d'=10 cm. Le faisceau retour est peu affecté par l'atmosphère. Reprendre les questions 4 à 10 dans ce cas (en faisant les applications numériques).
Dans ce problème on n'a pas tenu compte de l'absorption atmosphérique, du coefficient de réflexion des différents miroirs traversés, du rendement du détecteur qui compte les photons retour... tous ces facteurs diminuent encore la puissance reçue. En pratique, le nombre réel de photons reçus (hors les nombreux parasites) est d'environ 1 tous les 100 tirs. Pour plus d'information, voir le site web du Laser-Lune : http://wwwrc.obs-azur.fr/cerga/laser/laslune/llr.htm
Voir la solution
![]() et d'amplitude
et d'amplitude ![]() ayant traversé une ouverture circulaire de diamètre d. Cette onde se propage sur une distance D pour atteindre la Lune.
ayant traversé une ouverture circulaire de diamètre d. Cette onde se propage sur une distance D pour atteindre la Lune.
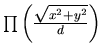 est
est