Licence de Physique LP2b -- Electromagnétisme et optique
Session de Septembre 2001
Partie II -- Optique
On considère l'interféromètre de la figure ci-dessous
constitué de deux lames semi-réfléchissantes  et
et 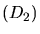 (transmettant chacune la moitié de l'amplitude de la lumière
incidente et réfléchissant l'autre moitié) et de deux
miroirs
(transmettant chacune la moitié de l'amplitude de la lumière
incidente et réfléchissant l'autre moitié) et de deux
miroirs 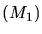 et
et 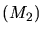 .
Une partie de la lumière incidente traverse les lames séparatrices
sans ètre déviée et parcourt en ligne droite le trajet
.
Une partie de la lumière incidente traverse les lames séparatrices
sans ètre déviée et parcourt en ligne droite le trajet 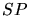 .
L'autre partie est déviée au point
.
L'autre partie est déviée au point 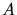 vers les miroirs et rejoint la première partie au point
vers les miroirs et rejoint la première partie au point 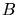 .
Les interférences sont observées sur l'écran
.
Les interférences sont observées sur l'écran 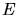 rapporté au repère
rapporté au repère 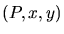 .
On appelle
.
On appelle 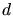 la distance
la distance 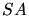 ,
, 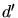 la distance
la distance 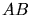 ,
, 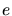 la distance
la distance 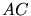 et
et 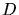 la distance
la distance 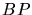 .
L'ensemble est éclairé par une source ponctuelle
.
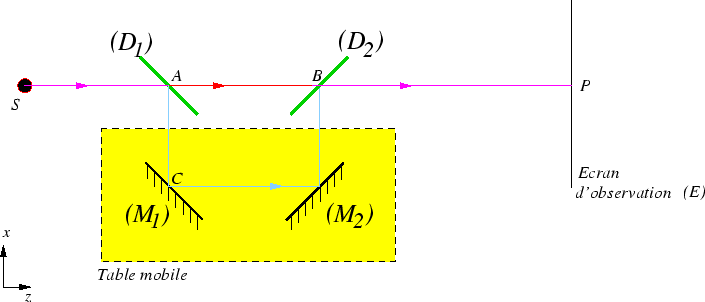
L'ensemble est éclairé par une source ponctuelle 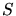 placée sur l'axe optique de l'interféromètre. en un
point pris comme origine des coordonnées. Dans tout le problème,
on se place dans les conditions de l'optique paraxiale.
placée sur l'axe optique de l'interféromètre. en un
point pris comme origine des coordonnées. Dans tout le problème,
on se place dans les conditions de l'optique paraxiale.
Première partie
-
Les deux miroirs sont montés sur une table mobile permettant d'introduire
une différence de marche variable entre les deux faisceaux. Dans
quel sens doit-elle alors se mouvoir ?
-
Chercher un problème équivalent plus simple faisant intervenir
la source
 et une source fictive
et une source fictive  .
Où ce trouve cette source
.
Où ce trouve cette source 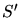 ? Faire un dessin du problème équivalent.
? Faire un dessin du problème équivalent.
-
On se place en un point
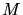 de coordonnées
de coordonnées 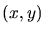 dans le plan
dans le plan 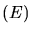 .
Calculer la différence de marche entre les rayons issus de
.
Calculer la différence de marche entre les rayons issus de 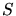 et
et 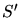 .
.
-
La source
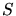 émet une radiation monochromatique de longueur
émet une radiation monochromatique de longueur 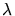 .
Calculer l'intensité au point
.
Calculer l'intensité au point 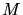 ,
décrire l'aspect du champ d'interférences. Faire un dessin.
,
décrire l'aspect du champ d'interférences. Faire un dessin.
-
On déplace la source
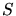 parallèlement à
parallèlement à 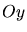 pour venir la mettre en un point situé en
pour venir la mettre en un point situé en 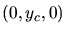 .
Comment est modifiée la figure d'interférences ?
.
Comment est modifiée la figure d'interférences ?
-
On éclaire l'interféromètre par deux sources ponctuelles
monochromatiques identiques,
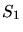 est placée sur l'axe optique en
est placée sur l'axe optique en 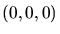 ,
, 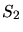 est placée en
est placée en 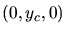 .
Les sources sont incohérentes entre elles. Ecrire l'intensité
dans le champ d'interférence (ne pas développer le calcul).
Dessiner schématiquement l'aspect du champ d'interférences.
.
Les sources sont incohérentes entre elles. Ecrire l'intensité
dans le champ d'interférence (ne pas développer le calcul).
Dessiner schématiquement l'aspect du champ d'interférences.
Seconde partie
La source 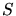 est à nouveau monochromatique et placée en
est à nouveau monochromatique et placée en 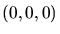 .
On place dans le trajet
.
On place dans le trajet 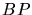 une lentille convergente de focale
une lentille convergente de focale 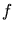 et on fait en sorte que l'écran
et on fait en sorte que l'écran 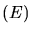 soit dans le plan focal image de la lentille. On appelle
soit dans le plan focal image de la lentille. On appelle 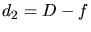 la distance entre le point
la distance entre le point 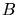 et le centre de la lentille.
et le centre de la lentille.
-
Ecrire sans calcul l'amplitude complexe de l'onde dans le plan de la lentille.
-
En déduire l'amplitude complexe dans le plan focal image
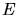 .
Calculer l'intensité de la figure d'interférences. Faire
un dessin. Comparer à la situation sans lentille de la première
partie.
.
Calculer l'intensité de la figure d'interférences. Faire
un dessin. Comparer à la situation sans lentille de la première
partie.
-
On déplace la source
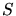 parallèlement à
parallèlement à 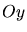 pour venir la mettre en un point situé en
pour venir la mettre en un point situé en 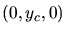 .
Comment est modifiée l'amplitude complexe dans le plan de la lentille
? La figure d'interférences sur l'écran
.
Comment est modifiée l'amplitude complexe dans le plan de la lentille
? La figure d'interférences sur l'écran 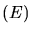 ?
?
-
On éclaire l'interféromètre par deux sources ponctuelles
monochromatiques identiques,
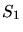 est placée sur l'axe optique en
est placée sur l'axe optique en 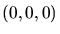 ,
, 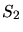 est placée en
est placée en 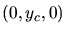 .
Les sources sont incohérentes entre elles. Ecrire l'intensité
dans le champ d'interférences. Comparer à celle de la question
6 de la première partie. Commentaires ?
.
Les sources sont incohérentes entre elles. Ecrire l'intensité
dans le champ d'interférences. Comparer à celle de la question
6 de la première partie. Commentaires ?
Rappels
On donne les transformées de Fourier suivantes :
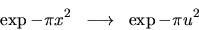
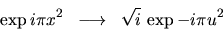
Voir la solution
![]() et
et ![]() (transmettant chacune la moitié de l'amplitude de la lumière
incidente et réfléchissant l'autre moitié) et de deux
miroirs
(transmettant chacune la moitié de l'amplitude de la lumière
incidente et réfléchissant l'autre moitié) et de deux
miroirs ![]() et
et ![]() .
Une partie de la lumière incidente traverse les lames séparatrices
sans ètre déviée et parcourt en ligne droite le trajet
.
Une partie de la lumière incidente traverse les lames séparatrices
sans ètre déviée et parcourt en ligne droite le trajet ![]() .
L'autre partie est déviée au point
.
L'autre partie est déviée au point ![]() vers les miroirs et rejoint la première partie au point
vers les miroirs et rejoint la première partie au point ![]() .
Les interférences sont observées sur l'écran
.
Les interférences sont observées sur l'écran ![]() rapporté au repère
rapporté au repère ![]() .
On appelle
.
On appelle ![]() la distance
la distance ![]() ,
, ![]() la distance
la distance ![]() ,
, ![]() la distance
la distance ![]() et
et ![]() la distance
la distance ![]() .
L'ensemble est éclairé par une source ponctuelle
.
L'ensemble est éclairé par une source ponctuelle ![]() placée sur l'axe optique de l'interféromètre. en un
point pris comme origine des coordonnées. Dans tout le problème,
on se place dans les conditions de l'optique paraxiale.
placée sur l'axe optique de l'interféromètre. en un
point pris comme origine des coordonnées. Dans tout le problème,
on se place dans les conditions de l'optique paraxiale.
