Correction de l'examen d'optique
Session de Septembre 2001
Première partie
-
La table doit se déplacer dans le sens des
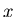
-
La source
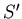 est sur l'axe
est sur l'axe 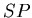 à une distance
à une distance 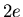 derrière
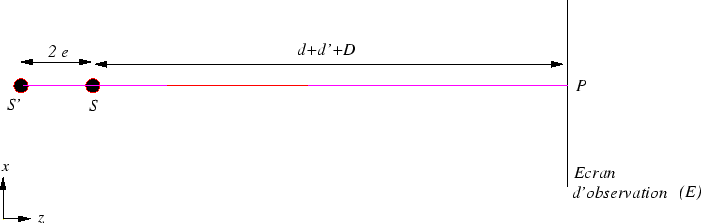
derrière 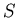 .
Dessin du problème équivalent :
.
Dessin du problème équivalent :
-
Différence de marche dans l'approximation paraxiale (
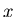 et
et 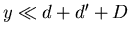 ):
):
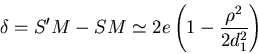
avec 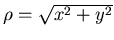 et en posant
et en posant 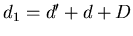 .
.
-
L'intensité sur l'écran s'écrit
![\begin{displaymath}I=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1-\frac{\rho^2}{2 d_1^2}\right) \right]\end{displaymath}](img11.gif)
L'aspect du champ d'interférences est un ensemble d'anneaux concentriques
centrés sur le point 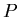 et qui se resserrent à mesure qu'on s'éloigne du centre.
Le problème est presque identique à celui de la source ponctuelle
se réfléchissant dans un miroir (à part le déphasage
de
et qui se resserrent à mesure qu'on s'éloigne du centre.
Le problème est presque identique à celui de la source ponctuelle
se réfléchissant dans un miroir (à part le déphasage
de 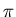 à la réflexion). Voir exemple
du cours . L'aspect de la figure est le suivant :
à la réflexion). Voir exemple
du cours . L'aspect de la figure est le suivant :

-
Si on déplace la source en
 ,
le centre de la figure d'interférences se décale aussi ;
le nouveau centre de la figure sera alors en
,
le centre de la figure d'interférences se décale aussi ;
le nouveau centre de la figure sera alors en  .
.
-
On additionne les intensités des franges produites par chaque source.
Ce qui donne
![\begin{displaymath}I=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1......\lambda} \left( 1-\frac{x^2+(y-y_c)^2}{2 d_1^2}\right) \right]\end{displaymath}](img15.gif)
Les deux constantes sont égales si les sources sont identiques.
On ne développera pas davantage les calculs. Il s'agit de deux réseaux
d'anneaux de centres distincts. L'aspect est le suivant (les franges verticales
sont perpendiculaires à l'écart entre les sources)

Seconde partie
-
En posant
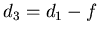 l'amplitude
l'amplitude 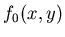 dans le plan de la lentille s'écrit
dans le plan de la lentille s'écrit
![\begin{displaymath}f_0(x,y)=\mbox{Cte}\; \cos \left[ \frac{4\pi e}{\lambda} \left( 1-\frac{\rho^2}{2 d_3^2}\right) \right]\end{displaymath}](img18.gif)
-
Par application directe du cours
l'amplitude complexe sur l'écran
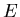 s'écrit
s'écrit
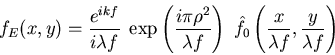
Ce qui donne (en développant le cosinus en deux exponentielles)
( Attention : la transformée de Fourier de 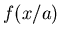 est
est 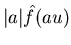 ,
ne pas oublier la valeur absolue).
,
ne pas oublier la valeur absolue).
![\begin{displaymath}f_E(x,y)=\mbox{Cte}\; \exp\left(\frac{i\pi\rho^2}{\lambda f}......} \left( 1+\frac{\rho^2 d_3^2}{8 e \lambda f^2}\right) \right]\end{displaymath}](img23.gif)
et l'intensité
![\begin{displaymath}I_E(x,y)=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1+\frac{\rho^2 d_3^2}{8 e \lambda f^2}\right) \right]\end{displaymath}](img24.gif)
C'est toujours un réseau de Soret comme dans le cas sans lentille.
Deux différences ici :
-
le signe - devant le terme en
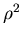 est devenu un + : inversion du contraste (les noirs remplacent les blancs)
est devenu un + : inversion du contraste (les noirs remplacent les blancs)
-
la taille des anneaux a changé (terme
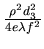 eu lieu de
eu lieu de 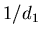 en facteur de
en facteur de 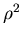 )
)
-
Si on déplace la source d'une quantité
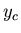 ,
l'amplitude complexe
,
l'amplitude complexe 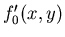 dans le plan d'entrée de la lentille change simplement d'origine
comme dans la première partie. On a alors
dans le plan d'entrée de la lentille change simplement d'origine
comme dans la première partie. On a alors
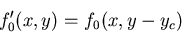
Dans le plan focal de la lentille, les propriétés de la
transformée de Fourier prévoient que l'amplitude complexe
sera affectée d'un terme de phase 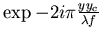 ,
l'intensité restant inchangée. Ainsi un déplacement
de la source ne change rien aux franges observées dans le plan focal
de la lentille, alors que sans la lentille les franges se déplacent
comme la source.
,
l'intensité restant inchangée. Ainsi un déplacement
de la source ne change rien aux franges observées dans le plan focal
de la lentille, alors que sans la lentille les franges se déplacent
comme la source.
-
L'intensité s'écrit comme la somme des intensités
produites par chacune des sources (elles sont incohérentes entre
elles). On a alors :
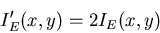

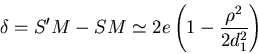
![]() et en posant
et en posant ![]() .
.
![\begin{displaymath}I=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1-\frac{\rho^2}{2 d_1^2}\right) \right]\end{displaymath}](img11.gif)
![]() et qui se resserrent à mesure qu'on s'éloigne du centre.
Le problème est presque identique à celui de la source ponctuelle
se réfléchissant dans un miroir (à part le déphasage
de
et qui se resserrent à mesure qu'on s'éloigne du centre.
Le problème est presque identique à celui de la source ponctuelle
se réfléchissant dans un miroir (à part le déphasage
de ![]() à la réflexion). Voir exemple
du cours . L'aspect de la figure est le suivant :
à la réflexion). Voir exemple
du cours . L'aspect de la figure est le suivant :

![\begin{displaymath}I=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1......\lambda} \left( 1-\frac{x^2+(y-y_c)^2}{2 d_1^2}\right) \right]\end{displaymath}](img15.gif)

![\begin{displaymath}f_0(x,y)=\mbox{Cte}\; \cos \left[ \frac{4\pi e}{\lambda} \left( 1-\frac{\rho^2}{2 d_3^2}\right) \right]\end{displaymath}](img18.gif)
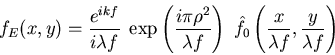
![\begin{displaymath}f_E(x,y)=\mbox{Cte}\; \exp\left(\frac{i\pi\rho^2}{\lambda f}......} \left( 1+\frac{\rho^2 d_3^2}{8 e \lambda f^2}\right) \right]\end{displaymath}](img23.gif)
![\begin{displaymath}I_E(x,y)=\mbox{Cte}\; \cos^2 \left[ \frac{4\pi e}{\lambda} \left( 1+\frac{\rho^2 d_3^2}{8 e \lambda f^2}\right) \right]\end{displaymath}](img24.gif)