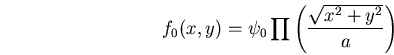L'intensité s'écrit
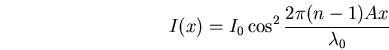
![]() est une constante réelle et positive. On note que
est une constante réelle et positive. On note que ![]() est indépendante de
est indépendante de ![]() .
.
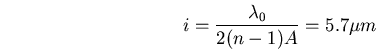
Au sens de Shannon il faut échantillonner les franges en
mettant deux pixels par frange, ce qui serait possible avec une caméra
possédant des pixels de 2.8 ![]() m.
Ici avec une taille de pixel de 15
m.
Ici avec une taille de pixel de 15 ![]() ,
les franges sont ``sous-échantillonnées'' : un seul pixel
voit plusieurs franges.
,
les franges sont ``sous-échantillonnées'' : un seul pixel
voit plusieurs franges.
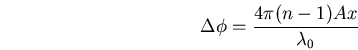
.La règle de trois habituelle ![]() permet de trouver la différence de marche équivalente
permet de trouver la différence de marche équivalente
. Le retard ![]() est égal au temps de parcours de
est égal au temps de parcours de ![]() à la vitesse de la lumière, donc
à la vitesse de la lumière, donc
-
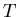 est un temps, en secondes
est un temps, en secondes -
C'est une question de cours (voir cette partie du cours ou celle-ci). Si on sépare
l'onde en deux en imposant à l'une des deux sous-ondes un retard
 ,
l'inteférence donnera des franges avec un contraste
,
l'inteférence donnera des franges avec un contraste 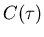 égal à
égal à 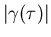 .
. 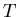 représente la largeur de la fonction
représente la largeur de la fonction 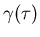 ,
c'est le temps de cohérence.
,
c'est le temps de cohérence. -
Le cas monochromatique est caractérisé par des interférences
de contraste constant quel que soit
 .
Ce qui correspond à
.
Ce qui correspond à 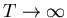 .
. -
D'après le cours, l'intensité des franges d'interférence
est donnée, en fonction de la variable
 par
par -
Le nombre
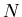 de franges visibles est simple à calculer sur
de franges visibles est simple à calculer sur 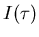 .
C'est le rapport de la largeur de la fonction
.
C'est le rapport de la largeur de la fonction 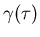 sur la période des franges. Ainsi
sur la période des franges. Ainsi -
Pour mesurer
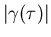 ,
il suffit de calculer localement le contraste des franges d'interférence
par la formule habituelle
,
il suffit de calculer localement le contraste des franges d'interférence
par la formule habituelle -
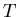 est le temps de cohérence ; il est par définition égal
à l'inverse de la largeur spectrale
est le temps de cohérence ; il est par définition égal
à l'inverse de la largeur spectrale 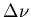 de la lumière. Exprimée en termes de longueur d'onde, cette
largeur spectrale
de la lumière. Exprimée en termes de longueur d'onde, cette
largeur spectrale 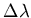 est
est -
L'onde est quasi-monochromatique, son spectre est de la forme
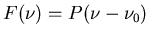 .
La fonction
.
La fonction 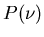 est le profil de raie, reliée au contraste des franges
est le profil de raie, reliée au contraste des franges 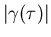 par la relation (voir cours)
par la relation (voir cours)
avec ![]() la fréquence de la lumière incidente. Ici
la fréquence de la lumière incidente. Ici ![]() d'après la question 3, et l'on obtient une expression de l'intensité
en fonction de l'abcisse
d'après la question 3, et l'on obtient une expression de l'intensité
en fonction de l'abcisse ![]()
![\begin{displaymath}I(x)=Cte \left[1+\exp\left(-\frac{2(n-1)A\vert x\vert}{cT}\r......\left(\frac{4\pi (n-1)A\vert x\vert}{\lambda_0}\right) \right]\end{displaymath}](img33.png)
quand ![]() on retrouve bien le cas monochromatique de la question 1.
on retrouve bien le cas monochromatique de la question 1.
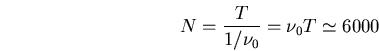
On remarque que ![]() ne dépend que des deux nombres
ne dépend que des deux nombres ![]() et
et ![]() qui sont caractéristiques de la lumière incidente et non
de l'expérience. Il est donc impossible de doubler
qui sont caractéristiques de la lumière incidente et non
de l'expérience. Il est donc impossible de doubler ![]() en sans modifier les propriétés de l'onde incidente.
en sans modifier les propriétés de l'onde incidente.
avec ![]() l'intensité au centre d'une frange brillante au voisinage du point
l'intensité au centre d'une frange brillante au voisinage du point ![]() et
et ![]() l'intensité au centre d'une frange sombre. Ce nombre
l'intensité au centre d'une frange sombre. Ce nombre ![]() est précisément égal au degré de cohérence
de l'onde (exprimé en fonction de la variable
est précisément égal au degré de cohérence
de l'onde (exprimé en fonction de la variable ![]() ).
Il suffit alors de faire une mesure en plusieurs points
).
Il suffit alors de faire une mesure en plusieurs points ![]() ,
, ![]() ,
...correspondants à des retards
,
...correspondants à des retards ![]() ,
, ![]() ,
...pour avoir une mesure de quelques valeurs de
,
...pour avoir une mesure de quelques valeurs de ![]() .
.

On a ainsi, à une constante près, le module de la
TF de la fonction ![]() .
Par ailleurs, l'argument du cosinus intervenant dans l'intensité
est de la forme
.
Par ailleurs, l'argument du cosinus intervenant dans l'intensité
est de la forme ![]() (voir cours) avec
(voir cours) avec ![]() la partie imaginaire de la TF de
la partie imaginaire de la TF de ![]() .
Ici on a
.
Ici on a ![]() et il apparait alors que
et il apparait alors que ![]() est une fonction réelle paire. On calcule facilement
est une fonction réelle paire. On calcule facilement ![]() par TF inverse ; il vient
par TF inverse ; il vient
et
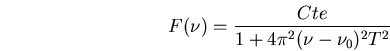
C'est une fonction lorentzienne de largeur ![]() centrée sur la fréquence
centrée sur la fréquence ![]() (typiquement une raie d'émission d'un gaz excité).
(typiquement une raie d'émission d'un gaz excité).