Licence de Physique LP2b -- Electromagnétisme et optique
Session de Septembre 2002
Partie II -- Optique
Les 2 exercices sont indépendants.
1. Biprisme
Une onde plane monochromatique de longueur d'onde 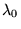 éclaire sous incidence normale un biprisme formé de deux
prismes identiques d'indice
éclaire sous incidence normale un biprisme formé de deux
prismes identiques d'indice 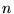 et d'angle faible
et d'angle faible 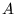 .
Chaque prisme est de largeur
.
Chaque prisme est de largeur 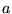 dans la direction
dans la direction 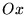 et de dimensions supposées infinies dans la direction
et de dimensions supposées infinies dans la direction 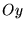 .
Pour
.
Pour 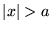 ,
un diaphragme opaque stoppe le passage de la lumière. Cet écran
est placé dans le plan
,
un diaphragme opaque stoppe le passage de la lumière. Cet écran
est placé dans le plan 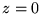 ,
on observe dans le plan
,
on observe dans le plan 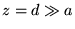 .
On donne les valeurs numériques suivantes :
.
On donne les valeurs numériques suivantes : 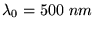 ,
, 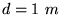 ,
, 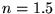 ,
, 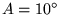 .
.
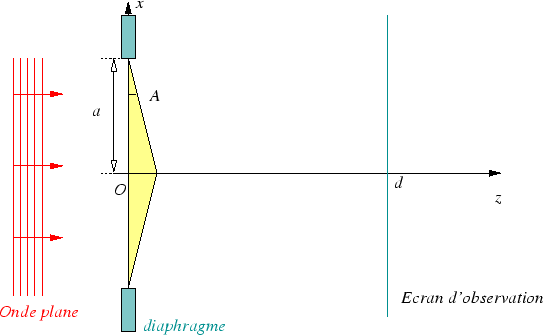
-
Dans tout le problème, on néglige la diffraction par les
bords des prismes. Montrer que chaque point du plan
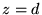 est éclairé par deux ondes provenant chacune d'un des prismes.
Ecrire à une constante multiplicative près l'intensité
dans le plan
est éclairé par deux ondes provenant chacune d'un des prismes.
Ecrire à une constante multiplicative près l'intensité
dans le plan 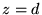 .
.
-
Calculez l'interfrange. On place dans le plan
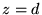 une caméra CCD avec des pixels de largeur 15
une caméra CCD avec des pixels de largeur 15 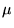 .
Les franges sont-elles bien échantillonnées (au sens de Shannon)
? Sinon, que suggérez-vous comme taille de pixels pour échantillonner
correctement ces franges ?
.
Les franges sont-elles bien échantillonnées (au sens de Shannon)
? Sinon, que suggérez-vous comme taille de pixels pour échantillonner
correctement ces franges ?
-
Quelle est la différence de phase
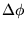 entre les deux ondes arrivant en un point d'abcisse
entre les deux ondes arrivant en un point d'abcisse 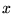 du plan
du plan 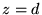 ? Ecrire la différence de marche
? Ecrire la différence de marche 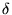 associée à
associée à 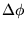 et le retard
et le retard 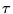 correspondant.
correspondant.
-
L'onde incidente, toujours plane et sous incidence normale, est cette fois
quasi-monochromatique autour de la longueur
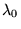 .
Elle possède un degré complexe de cohérence normalisé
.
Elle possède un degré complexe de cohérence normalisé 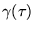 dont le module vaut
dont le module vaut 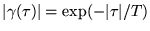 avec
avec 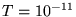 S.I.
S.I.
-
Quelle est la dimension de
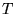 (quelle unité SI) ?
(quelle unité SI) ?
-
Rappeler en quelques lignes (pas de calculs !) la signification physique
de
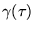 et de
et de 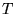 .
.
-
A votre avis, le cas parfaitement monochromatique correspond-il à
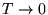 où à
où à 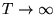 ? Pourquoi ?
? Pourquoi ?
-
Ecrire, à une constante multiplicative près, l'intensité
dans le plan
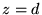 (on pourra se servir de la relation entre
(on pourra se servir de la relation entre 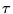 et
et 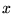 obtenue dans la question 3). Vérifiez que vous retrouvez le cas
monochromatique de la première question en faisant tendre
obtenue dans la question 3). Vérifiez que vous retrouvez le cas
monochromatique de la première question en faisant tendre 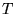 vers la valeur adéquate.
vers la valeur adéquate.
-
Combien de franges sont visibles ? Peut-on modifier l'expérience
pour doubler ce nombre de franges visibles sans toucher aux propriétés
de la lumière incidente ?
-
Proposez une méthode pour mesurer
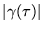 à partir des franges dans le plan
à partir des franges dans le plan 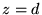 .
.
-
Donnez, en fonction des grandeurs définies dans l'énoncé,
un ordre de grandeur de la largeur spectrale
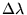 de la lumière incidente.
de la lumière incidente.
-
Calculer, à une constante multiplicatice près, le spectre
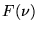 de la lumière incidente en fonction de la fréquence
de la lumière incidente en fonction de la fréquence 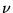 (on appellera
(on appellera 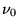 la fréquence associée à la longueur d'onde
la fréquence associée à la longueur d'onde 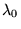 )
)
On rappelle les TF suivantes :
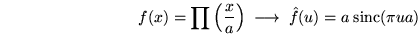
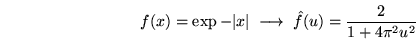
Voir la solution
2. Diffraction de Fresnel
Un trou circulaire de diamêtre 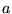 est éclairé sous incidence normale par une onde plane monochromatique
de longueur d'onde
est éclairé sous incidence normale par une onde plane monochromatique
de longueur d'onde 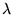 se propageant vers les
se propageant vers les 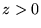 et d'amplitude
et d'amplitude 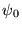 dans le plan
dans le plan 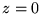 .
Ce trou est placé dans le plan
.
Ce trou est placé dans le plan 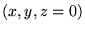 .
Calculer, dans l'approximation paraxiale, l'intensité diffractée
par ce masque en tout point de coordonnées
.
Calculer, dans l'approximation paraxiale, l'intensité diffractée
par ce masque en tout point de coordonnées 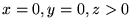 (donc sur l'axe optique).
(donc sur l'axe optique).
Voir la solution

