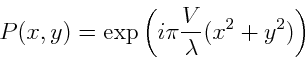Filtrage d'une mire
sinusoïdale par un filtre de phase
On considère une mire sinusoïdale dont le coefficient de transmission s'écrit :
avec 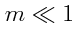 . La mire est éclairée sous incidence
normale par une onde plane monochromatique, le schéma de
l'expérience est un montage 4f classique identique à
celui de cet exercice.
. La mire est éclairée sous incidence
normale par une onde plane monochromatique, le schéma de
l'expérience est un montage 4f classique identique à
celui de cet exercice.
- Quelles sont les fréquences spatiales présentes dans la mire ? La mire est placée dans le plan
 . Calculer l'intensité
. Calculer l'intensité 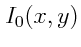 dans ce plan et donner son contraste.
dans ce plan et donner son contraste.
- Calculer l'amplitude complexe de l'onde dans le plan
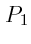 .
.
- Dans le plan de filtrage
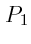 on place un masque de phase dont la transmission
on place un masque de phase dont la transmission 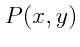 s'écrit
s'écrit
. Quelle est la nature de ce masque et quelle est la signification de 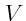 ?
?
- Ecrire l'amplitude complexe et l'intensité dans le plan
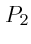 .
.
- Quelles sont les valeurs de
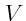 pour lesquelles l'intensité est uniforme dans le plan
pour lesquelles l'intensité est uniforme dans le plan 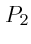 ?
?
- Donner le contraste de l'intensité et montrer que le contraste s'inverse pour certaines valeurs de
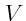 .
.
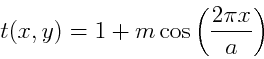
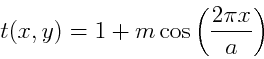

![]() . La mire est éclairée sous incidence
normale par une onde plane monochromatique, le schéma de
l'expérience est un montage 4f classique identique à
celui de cet exercice.
. La mire est éclairée sous incidence
normale par une onde plane monochromatique, le schéma de
l'expérience est un montage 4f classique identique à
celui de cet exercice.