Relation objet - objet filtré

Le montage optique est le même que dans le paragraphe précédent.

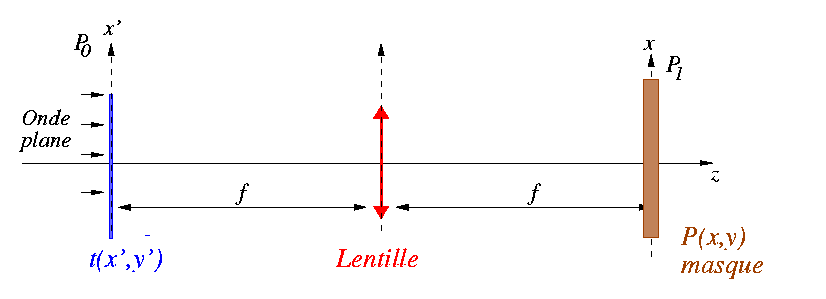
On note (x',y') les coordonnées d'un point dans le plan P₀ et (x,y) les coordonnées d'un point dans le plan P₁.
L'objet t(x',y') est placé au foyer objet de la lentille (plan P₀). L'amplitude de l'onde incidente dans le plan P₀ est $\psi_0$ . Au foyer image de la lentille (plan P₁) on place un masque de coefficient de transmission P(x,y).

L'amplitude dans le plan P₁ est donnée par l'équation (5) :

$\begin{displaymath}f_1(x,y)=\psi_0 \; \frac{e^{2 i k f}}{i\lambda f} \; \hat t\left(\frac{x}{\lambda f},\frac{y}{\lambda f} \right) \end{displaymath}$

dans le plan P₁ on effectue le filtrage donc on multiplie cette amplitude par P(x,y) pour obtenir une amplitude filtrée $\tilde f(x,y)$

$\begin{displaymath}\tilde f(x,y)=f_1(x,y)\; P(x,y)\; = \; \psi_0 \; \frac{e^{2 i... ...left(\frac{x}{\lambda f},\frac{y}{\lambda f} \right) \; P(x,y) \end{displaymath}$

ce qui s'écrit aussi, en introduisant le coefficient de transmission de l'objet filtré t_f(x',y')

$\begin{displaymath}\hat f(x,y)=\psi_0 \; \frac{e^{2 i k f}}{i\lambda f} \; \hat t_f\left(\frac{x}{\lambda f},\frac{y}{\lambda f} \right) \end{displaymath}$

il vient

$\begin{displaymath}\hat t_f\left(\frac{x}{\lambda f},\frac{y}{\lambda f} \right)... ...\left(\frac{x}{\lambda f},\frac{y}{\lambda f} \right)\; P(x,y) \end{displaymath}$

d'où la relation de filtrage linéaire entre les transformées de Fourier de t et t_f

$\begin{displaymath}\mbox{\fbox{$\displaystyle \hat t_f(u,v) \; = \; \hat t(u,v)\; P(\lambda f u,\lambda f v) $ } }\end{displaymath}$

(7)

la fonction $P(\lambda f u,\lambda f v)$ est la fonction de transfert du filtrage. En repassant dans le plan réel on obtiendra une relation de convolution entre t et t_F. On fait une TF inverse de l'équation précédente :

$\begin{displaymath}t_f(x,y) \; = \; t(x,y)\; \ast \; {\cal F}^{-1}\left\{ P(\lambda f u,\lambda f v)\right\} \end{displaymath}$

et compte tenu du fait que ${\cal F}^{-1}\left\{f(u)\right\}=\hat f(-x)$ , on obtient

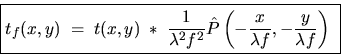$\begin{displaymath}\mbox{\fbox{$\displaystyle t_f(x,y) \; = \; t(x,y)\; \ast \;... ... P\left(-\frac{x}{\lambda f},-\frac{y}{\lambda f} \right) $ } }\end{displaymath}$

(8)

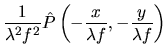la fonction $\displaystyle \frac{1}{\lambda^2 f^2} \hat P\left(-\frac{x}{\lambda f},-\frac{y}{\lambda f} \right)$ est la réponse impulsionnelle du filtrage.