-
Les deux ondes sont planes, de vecteurs d'ondes orientés suivant
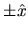 ; leurs amplitudes complexes s'écrivent dans le champ d'interférences
; leurs amplitudes complexes s'écrivent dans le champ d'interférences
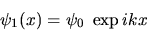
et
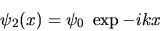
ce qui donne une intensité
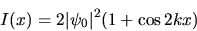
interfrange 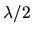 ,
contraste 1.
,
contraste 1.
-
Entre les deux ondes existe maintenant une différence de marche
à l'origine
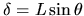 dûe au fait qu'un front d'onde incident atteint le télescope
1 après le télescope 2. L'intensité devient :
dûe au fait qu'un front d'onde incident atteint le télescope
1 après le télescope 2. L'intensité devient :
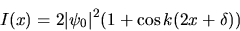
l'interfrange et le contraste sont inchangés, l'origine se décale
de 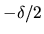 (vers la gauche sur le dessin)
(vers la gauche sur le dessin)
-
Onde quasi-monochromatique : le terme en cosinus est multiplié par
un contraste
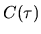 d'épendant du retard entre les deux ondes en un point
d'épendant du retard entre les deux ondes en un point 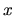 du champ d'interférences :
du champ d'interférences : 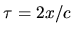 (
(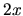 et pas simplement
et pas simplement 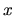 : à
: à 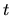 si un front d'onde de
si un front d'onde de 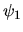 se trouve en
se trouve en 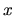 ,
le front d'onde correspondant de
,
le front d'onde correspondant de 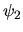 se trouve en
se trouve en 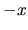 ,
la différence de marche entre les deux est
,
la différence de marche entre les deux est 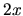 ).
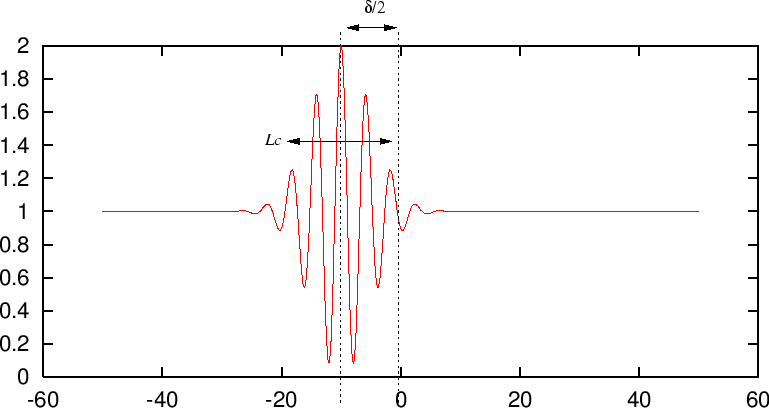
La demi-largeur de
).
La demi-largeur de 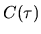 est le temps de cohérence ; le changement de variable
est le temps de cohérence ; le changement de variable 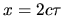 montre que le contraste des franges, exprimé en fonction de
montre que le contraste des franges, exprimé en fonction de 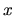 dans le champ d'interférences a une largeur
dans le champ d'interférences a une largeur 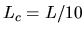 (longueur de cohérence). Le champ d'interférences présentera
donc des franges de contraste décroissant, dans une zône de
largeur
(longueur de cohérence). Le champ d'interférences présentera
donc des franges de contraste décroissant, dans une zône de
largeur 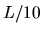 autour du point
autour du point 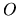 .
.
-
Même raisonnement que précédemment, le retard entre
les deux ondes en un point
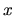 est
est 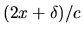 .
Le paquet de franges se décale de
.
Le paquet de franges se décale de 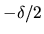 .
Le point
.
Le point 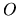 reste dans le paquet de franges si le décalage d'origine
reste dans le paquet de franges si le décalage d'origine 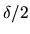 est inférieur à la demi largeur du paquet
est inférieur à la demi largeur du paquet 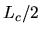 .
Soit si
.
Soit si 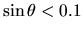 ce qui donne une plage de distances zénitales comprises dans un
intervalle de
ce qui donne une plage de distances zénitales comprises dans un
intervalle de 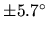 autour du zénith.
autour du zénith.
-
L'origine des franges est située en
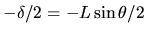 et se déplace à la vitesse
et se déplace à la vitesse 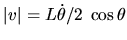 .
Pour une source au zénith (
.
Pour une source au zénith (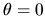 )
avec les valeurs proposées on obtient
)
avec les valeurs proposées on obtient 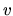 =3.6
mm/s
=3.6
mm/s
![]()
![]() ,
contraste 1.
,
contraste 1.
![]() (vers la gauche sur le dessin)
(vers la gauche sur le dessin)


![]()
![]() ,
contraste 1.
,
contraste 1.
![]() (vers la gauche sur le dessin)
(vers la gauche sur le dessin)

