Licence de Physique -- Interrogation d'optique II
Sans document - durée 30 mn
Date: 21 Octobre 2008
Un masque percé de trois trous carrés de côté 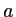 est éclairé sous incidence normale par une onde électromagnétique plane de longueur d'onde
est éclairé sous incidence normale par une onde électromagnétique plane de longueur d'onde  . On note
. On note  l'amplitude complexe incidente dans le plan du masque pris comme origine des
l'amplitude complexe incidente dans le plan du masque pris comme origine des  . Les trous sont centrés sur les positions
. Les trous sont centrés sur les positions  ,
,  et
et  (avec
(avec  ).
).
Le but de l'exercice est de calculer l'intensité dans un plan  en se plaçant dans l'approximation du champ lointain (diffraction à l'infini,
en se plaçant dans l'approximation du champ lointain (diffraction à l'infini,  ).
).
- Ecrire le coefficient de transmission du masque dans le plan
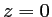 .
.
- Calculer l'intensité
 dans le plan
dans le plan  . Faire apparaitre une somme de cosinus.
. Faire apparaitre une somme de cosinus.
- On se place dans l'hypothèse où
 .
.
- Ecrire l'intensité dans ce cas. Cette fonction est périodique. Quelle est sa période
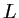 ?
?
- Calculer les valeurs de
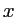 où la dérivée de l'intensité s'anulle dans l'intervalle
où la dérivée de l'intensité s'anulle dans l'intervalle 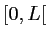 (on rappelle que
(on rappelle que
 , que
, que
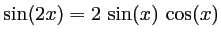 et que
et que
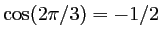 )
)
- En déduire l'emplacement des franges sombres (dans l'intervalle
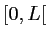 ).
).
- De même pour les franges brillantes. Mettre en évidence la présence de maxima principaux et secondaires de l'intensité et préciser la position de ces maxima dans l'intervalle
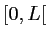 .
.
- Tracer la courbe de l'intensité
 dans l'intervalle
dans l'intervalle
![$ [-2 L, 2 L]$](img22.gif) (faire apparaitre les abcisses et les ordonnées des maxima et minima sur les axes).
(faire apparaitre les abcisses et les ordonnées des maxima et minima sur les axes).
On donne les transformées de Fourier suivantes :

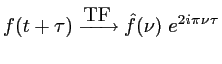
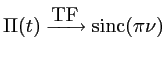
Voir la solution
![\includegraphics[width=10cm]{3trous.eps}](img9.gif)
![\includegraphics[width=10cm]{3trous.eps}](img9.gif)
![]() en se plaçant dans l'approximation du champ lointain (diffraction à l'infini,
en se plaçant dans l'approximation du champ lointain (diffraction à l'infini, ![]() ).
).