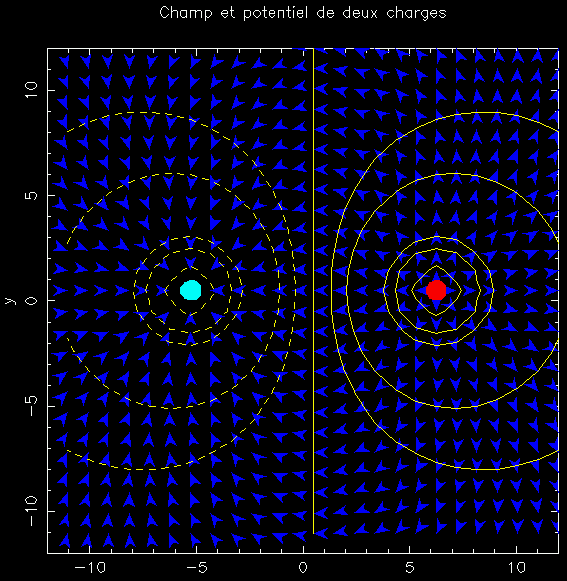



Exemple 4 :
Tracé d'un champ de vecteurs
Principe
Soit E un champ de vecteurs dans le plan (x,y) représenté par ses composantes cartésiennes Ex(x,y) et Ey(x,y). E représente par exemple le champ électrique d'un fil infini dans le plan perpendiculaire au fil.
PgPlot fournit une fonction cpgvect qui permet de tracer le champ de vecteurs sous la forme de petites flèches. Les valeurs de Ex et Ey doivent ètre discrétisées sur deux tableaux bidimensionnels. PgPlot dessine une flèche à chaque point du tableau.
Le programme ci-dessous dessine le champ de deux charges ponctuelles égales et opposées, et superpose les équipotentielles dessinées au moyen de la fonction cpgcont. On dessine également deux cercles colorés à l'emplacement des charges.
*
/**************************************************************
vector.c
Dessine un champ de vecteurs definis par
ses deux composantes cartesiennes
ici, champ d'un couple de charges aligne suivant
Ox
**************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "/usr/include/cpgplot.h"
#define MAX(a,b) ( (a)>(b) ? (a) : (b))
#define MIN(a,b) ( (a)<(b) ? (a) : (b))
main()
{
int i,j;
/* indices de boucle */
int dimx=25,dimy=25;
/* nb de points en x et en y */
float ex[dimx*dimy],ey[dimx*dimy],v[dimx*dimy];
/* composantes du champ de vecteurs et potentiel */
float x,y;
/* variables intermediaires pour le calcul */
float xmin,xmax;
/* intervalle. en x */
float ymin,ymax;
/* intervalle. en y */
float tr[6];
/* matrice utilisee par pgvect */
float d1,d2,d=12,nc=11;
float contours[11]={-0.8, -0.4, -0.3, -0.1,
-0.05, 0., 0.05, 0.1, 0.3, 0.4, 0.8}; /* equipot. values */
/* Remplissage des tableaux de valeurs
-----------------------------------
*/
for (i=0; i<dimy; i++)
for (j=0; j<dimx; j++)
{
x=j-dimx/2
; /* passage pixels -> (x,y) */
y=i-dimy/2;
d1=hypot(x-d/2,y);
d2=hypot(x+d/2,y);
ex[i*dimx+j]=(x-d/2)/d1/d1/d1-(x+d/2)/d2/d2/d2;
ey[i*dimx+j]=y/d1/d1/d1-y/d2/d2/d2;
v[i*dimx+j]=1/d1-1/d2;
}
/* Bornes
------ */
xmin=-dimx/2; xmax=dimx/2;
ymin=-dimy/2; ymax=dimy/2;
/* Matrice de passage pixels -> coordonnees
user
---------------------------------------------
*/
tr[0]=xmin;
tr[1]=(xmax-xmin)/dimx;
tr[2]=0;
tr[3]=ymin;
tr[4]=0;
tr[5]=(ymax-ymin)/dimy;
/* Plot champ de vecteurs
---------------------- */
cpgopen("?");
cpgenv(xmin,xmax,ymin,ymax,1,0);
/* JUST=1 : repere orthonorme */
cpglab("x","y","Champ et potentiel de deux
charges");
cpgsci(4);
cpgvect(ex,ey,dimx,dimy,1,dimx,1,dimy,0.5,-4,tr,0);
/* Plot isocontours potentiel
--------------------------
*/
cpgsci(7);
cpgcont(v,dimx,dimy,1,dimx,1,dimy,contours,nc,tr);
/* Plot charges
------------ */
cpgsci(2);
cpgcirc(d/2+0.25,0.5,0.5);
cpgsci(5);
cpgcirc(-d/2+0.75,0.5,0.5);
cpgend();
}
