| <<< back | large-scale statistics of passive scalar transport |
|
A passive scalar is a quantity that is transported by the flow but does not back react on
it. This scheme can be used to describe real scalar transport in the case where the back
reaction of the scalar on the velocity field is negligible.
Scalar structures are bound to decay in the absence of an external source of fluctuations.
If an external pumping is considered, at scales smaller than the injection lenghtscale, a flux
of scalar fluctuations develops. In this range of scales the passive scalar phenomenology strongly resembles that of hydrodynamic turbulence, hence the expression “scalar
turbulence”. On the contrary, thermal equilibrium is expected at scales larger than the
injection scale, where no upscale flux is present. Surprisingly enough, this is not the general
case. |
||
|
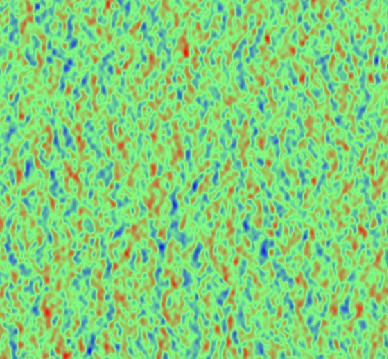
Snapshot of the scalar field obtained by direct numerical simulation of transport by a Kraichnan velocity field. Here the anisotropy has been introduced at a very small scale, but, due to the presence of long-range correlations, it propagates toward large scales (as it can be seen from the snapshot). |
 |
We obtained the same results for the case of real advecting flows, by means of direct numerical simulation of two-dimensional turbulence in the inverse cascade regime, advecting a passive scalar forced at small scales. |
||