Considérons un objet émetteur de lumière possédant une répartition d'intensité O(x,y) en fonction de la position angulaire (x,y). Lorsqu'une image est faite de cet objet par un télescope ou un système quelconque, les propriétés d'addition linéaire des intensités en éclairage incohérent permettent d'écrire l'intensité reçue en un point (x',y') du plan focal :
où S(x,y ; x',y') est une fonction qui dépend du télescope et qui exprime l'étalement de chaque point de l'objet dans l'image.
Si le système est invariant par translation, S ne dépend que de x-x' et de y-y' . La relation ci-dessus se ramène à une simple convolution :
Si l'objet observé est une étoile ponctuelle assimilable à un pic de Dirac, l'image observée est I=S. On appelle S la réponse impulsionnelle de l'instrument. Dans l'approximation de la diffraction de Fraunhoffer, S est simplement donnée par le carré du module de la transformée de Fourier de l'amplitude complexe sur la pupille de l'instrument [43]. Dans un télescope circulaire de diamètre D, c'est la fameuse tache d'Airy :
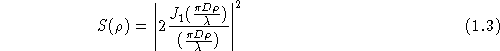
La transformée de Fourier de la fonction S est la fonction de transfert de l'instrument et mesure le degré de redondance de chaque fréquence spatiale dans l'image. Elle est donnée par l'autocorrélation de la pupille, c'est à dire la surface de recouvrement de deux pupilles identiques décalées d'une quantité f. Pour un télescope circulaire de diamètre D la fonction de transfert est égale à [43] :
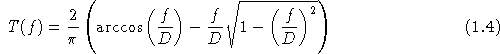
Son graphe est représenté en figure 
. Cette fonction s'annule au point 
; par conséquent le télescope ne permet pas de percevoir des détails inférieurs à 
: c'est le fameux pouvoir séparateur dont nous avons déjà parlé. C'est par exemple à cause de lui que nous ne voyons pas la structure atomique des objets.
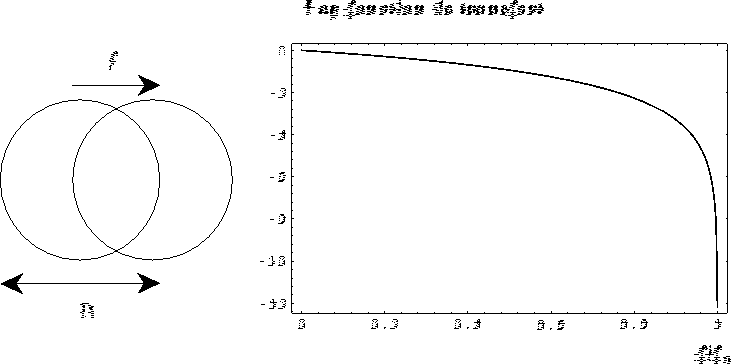
Figure: Fonction de transfert d'une pupille circulaire : elle mesure l'importance avec laquelle une fréquence spatiale f est transmise à l'image. Elle est égale au recouvrement des aires de deux pupilles décalées d'une quantité f. Elle s'annule pour les valeurs supérieures à : on parle de fréquence de coupure du télescope.