L'histogramme des images de l'étoile de référence des reproduit sur la figure 
. On remarque qu'il présente une zone assez linéaire sur sa plus grande partie, en bon accord avec le modèle gaussien, ce aui n'était pas évident a priori au vu de la large bande passante utilisée (la figure est en échelle logarithmique). Il y a par contre une remontée très nette quand on se rapproche de l'origine. Cette remontée peut être dûe à l'extension finie des champs de speckles qui sont, sur les images, entourés d'une zone de fond de ciel qui contribue de manière significative aux faibles valeurs de l'intensité. Si la densité de probabilité avait été calculée sur une zone réduite des images, cette remontée aurait sans doute été fortement atténuée. On remarque aussi que le maximum de la fonction n'est pas pour I=0 comme on aurait pu s'y attendre, mais il semble exister un offset qui décale globalement toutes les valeurs de l'intensité et trahit peut-être la présence d'un bruit additif. Le comportement de la courbe pour ces tout premiers points peut aussi être dû à des problèmes de flat-field ou toute autre cause inconnue. Ce comportement était en tout cas observé sur l'étoile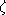 
Aqr en infrarouge [7] et manifestait ainsi la présence d'un bruit additif très important. On ne dispose malheureusement pas d'images de fond de ciel qui nous permettraient d'estimer la statistique du bruit. On peut cependant en avoir une première approximation en l'estimant sur des zones en bordure d'image loin des speckles. La présence d'un tel bruit se traduirait par une convolution des densités de probabilité du signal et du bruit.
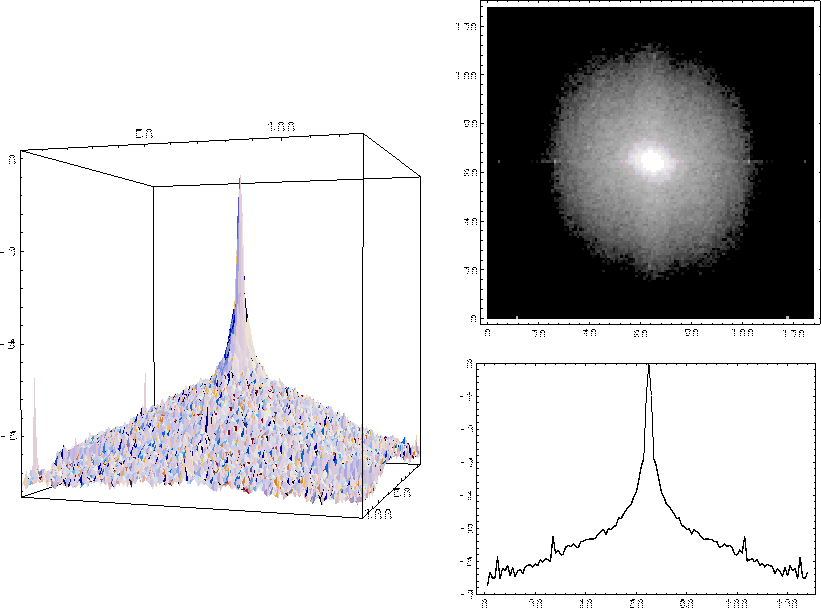
Figure: Densité spectrale de puissance de l'étoile de référence HD 218142. A gauche, représentation en pespactive cavalière. En haut à droite, représentation en échelle de gris ; et en bas à droite, on a effectué une coupe suivant la direction Ox. Les courbes sont représentées en échelle logarithmique
La densité spectrale des images de l'étoile de référence a été représentée en figure . Il semble que le plateau des hautes fréquences soit affaibli d'un facteur proche du million par rapport à la fonction de transfert hors atmosphère. Celle valeur correspondrait à un paramètre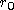 
de deux millimètres qui n'est pas très réaliste. Cependant il faut tenir compte du fait que le temps d'intégration de 1/60ème de seconde peut suffire à brouiller les images si la turbulence est forte (c'est d'ailleurs ce que semble montrer l'examen visuel des images) et que la bande passante utilisée était large.
Il est par contre intéressant de constater l'absence du biais qui caractérise le comptage de photons. Ce biais ayant pour valeur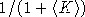 
où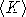 
est le nombre moyen de photons par images, on peut en déduire que les images contiennent plus de dix millions de photons et peuvent donc être considérées comme des images à fort flux. Une procédure de transformation inverse de Poisson n'est pas nécessaire dans ce cas.