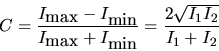Interférence de deux ondes sphériques
On considère deux ondes sphériques d'amplitudes complexes 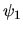 et
et 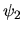 ,
de sources
,
de sources 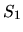 et
et 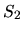 ,
monochromatiques et de même longueur d'onde
,
monochromatiques et de même longueur d'onde 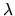 .
Les sources sont placées dans le plan
.
Les sources sont placées dans le plan 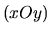 en
en 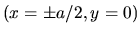 .
On observe sur un écran placé à une distance
.
On observe sur un écran placé à une distance 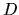 du plan des sources l'intensité résultant de l'interférence
de ces deux ondes. La géométrie du problème est celle
de la figure ci-dessous.
du plan des sources l'intensité résultant de l'interférence
de ces deux ondes. La géométrie du problème est celle
de la figure ci-dessous.
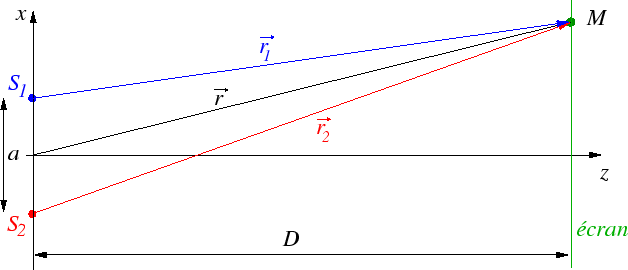
L'amplitude complexe des deux ondes s'écrit en un point 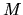 du champ d'interférences (avec
du champ d'interférences (avec 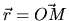 )
:
)
:
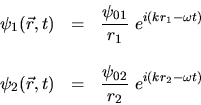
où 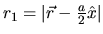 et
et 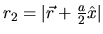 désignent les distances entre le point courant et les sources.
désignent les distances entre le point courant et les sources.
Calcul de l'intensité dans le plan 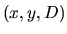
Comme toujours on calcule l'intensité moyennée sur
le temps de pose du détecteur utilisé pour observer les interférences,
par exemple l'oeil ou une caméra. Soit 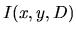 l'intensité résultant de l'interférence des deux ondes,
l'intensité résultant de l'interférence des deux ondes, 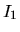 et
et 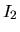 les intensités qui seraient produites par les sources
les intensités qui seraient produites par les sources 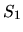 et
et 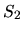 seules. On a alors (cf. paragraphe ``intensité
d'une onde'') :
seules. On a alors (cf. paragraphe ``intensité
d'une onde'') :
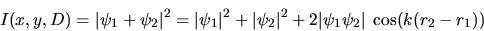
Soit
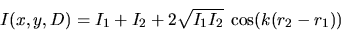
C'est une somme de trois termes :
Allure de la distribution d'intensité
Dans le cas général (pas de condition sur 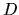 ),
les lignes d'iso-intensité sont données par les lignes de
crète du cosinus, soit
),
les lignes d'iso-intensité sont données par les lignes de
crète du cosinus, soit
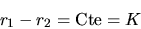
En développant 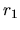 et
et 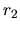 ,
,
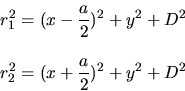
on obtient après quelques lignes de calcul l'équation
des lignes d'iso-intensité, c'est l'équation d'une famille
d'hyperboles dans le plan 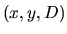 :
:
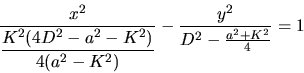
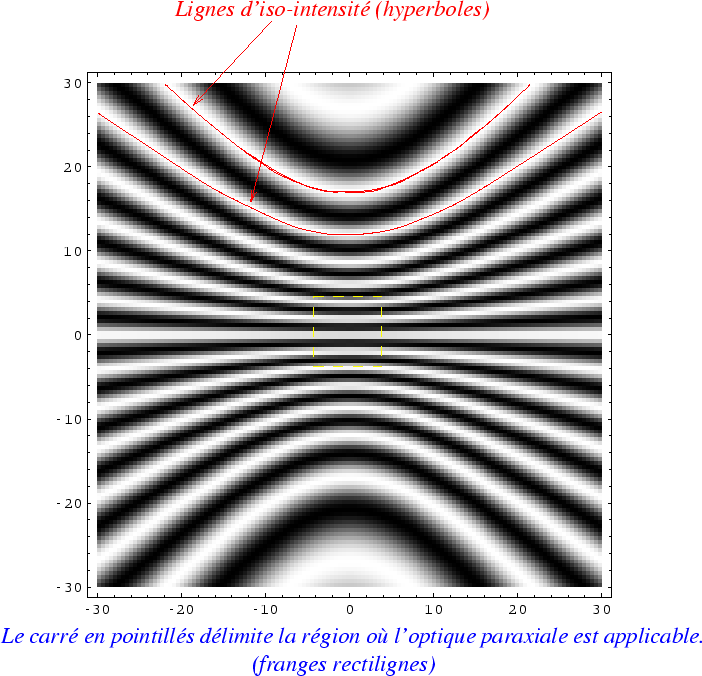
La figure ci-dessous donne l'allure du champ d'interférences.
Approximation paraxiale

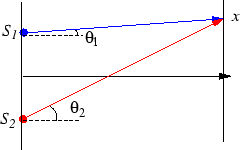
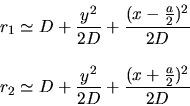
d'où
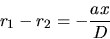
et l'intensité devient
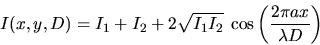
Les franges sont cette fois rectilignes, alignées avec l'axe 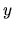 .
Deux quantités caractérisent ces franges :
.
Deux quantités caractérisent ces franges :
Il mesure la visibilité des franges. Un contraste de 1 décrit
une figure où les franges noires sont d'intensité nulle,
tandis qu'un contraste nul traduit une teinte unforme. Une figure de contraste
intermédiaire apparait striée de franges grisâtres,
d'autant plus grisâtres que le contraste tend vers 0.
Suivant : Interférences
d'une onde plane avec elle-même


![]() du champ d'interférences (avec
du champ d'interférences (avec ![]() )
:
)
:
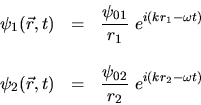
![]() et
et ![]() désignent les distances entre le point courant et les sources.
désignent les distances entre le point courant et les sources.
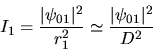
![]() )
et présente des oscillations conduisant à l'observation d'une
figure d'interférence striée de franges brillantes et sombres.
)
et présente des oscillations conduisant à l'observation d'une
figure d'interférence striée de franges brillantes et sombres.![]() et
et ![]() ,
,
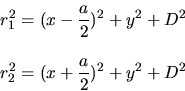
![]() :
:
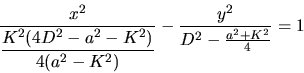



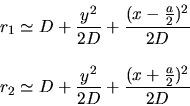
![]() .
Deux quantités caractérisent ces franges :
.
Deux quantités caractérisent ces franges :
![]() étant l'angle sous lequel sont vues les sources
étant l'angle sous lequel sont vues les sources ![]() et
et ![]() depuis le plan d'interférences
depuis le plan d'interférences