Interféromètre de Michelson
Le dispositif est celui de la figure suivante. Une onde incidente 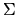 arrive sur une lame séparatrice sous une incidence de 45
arrive sur une lame séparatrice sous une incidence de 45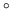 .
La moitié de cette onde (
.
La moitié de cette onde (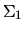 )
se réfléchit vers le miroir
)
se réfléchit vers le miroir 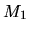 ,
l'autre moitié (
,
l'autre moitié (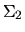 )
traverse la séparatrice et va se réfléchir sur le
miroir à translation réglable
)
traverse la séparatrice et va se réfléchir sur le
miroir à translation réglable 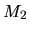 .
Les deux ondes reviennent sur la séparatrice. La encore, elles se
séparent en deux parties, mais on ne s'intéresse qu'aux parties
qui vont vers le champ d'interférences (plan
.
Les deux ondes reviennent sur la séparatrice. La encore, elles se
séparent en deux parties, mais on ne s'intéresse qu'aux parties
qui vont vers le champ d'interférences (plan 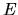 ).
).
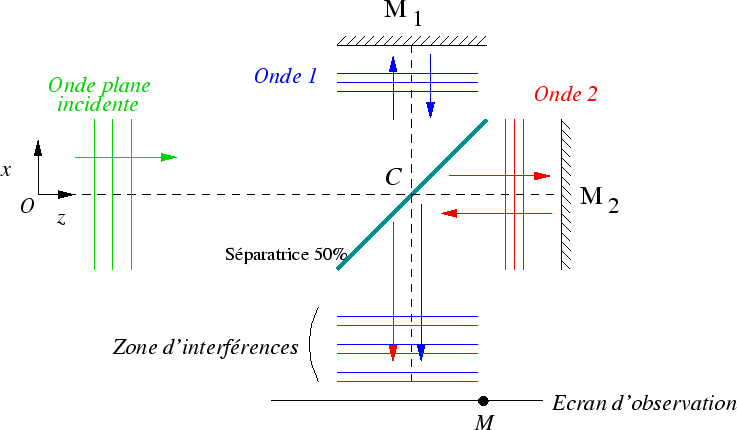
Schéma de principe d'un interféromètre de Michelson.
Une onde incidente (ici plane) éclaire une lame séparatrice
de centre 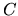 .
Une partie de l'onde est réfléchie (ici 50% de l'amplitude)
vers un miroir
.
Une partie de l'onde est réfléchie (ici 50% de l'amplitude)
vers un miroir 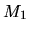 ,
puis revient vers la séparatrice et la traverse (à nouveau
une perte de 50% de l'amplitude). L'autre partie de l'onde incidente est
transmise vers le miroir réglable
,
puis revient vers la séparatrice et la traverse (à nouveau
une perte de 50% de l'amplitude). L'autre partie de l'onde incidente est
transmise vers le miroir réglable 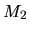 ,
revient vers la séparatrice et se réfléchit en partie
vers l'écran d'observation. Dans cet exemple on observe une intensité
uniforme (teinte plate).
,
revient vers la séparatrice et se réfléchit en partie
vers l'écran d'observation. Dans cet exemple on observe une intensité
uniforme (teinte plate).
Les applications de l'interféromètre de Michelson sont
vastes ; dans cet exemple on se limitera à une onde incidente plane
monochromatique. Les notations de cet exemple sont les suivantes :
-
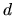 : distance
: distance 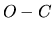 (
(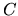 est le centre de la séparatrice)
est le centre de la séparatrice)
-
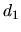 : distance
: distance 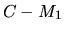
-
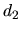 : distance variable
: distance variable 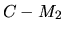
-
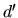 : distance entre
: distance entre 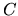 et le centre du plan
et le centre du plan 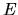
-
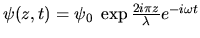 : amplitude complexe de l'onde
: amplitude complexe de l'onde 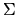
-
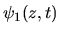 : amplitude complexe de l'onde
: amplitude complexe de l'onde 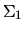
-
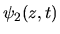 : amplitude complexe de l'onde
: amplitude complexe de l'onde 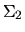
Les problèmes faisant intervenir des réflexions sur des miroirs
se traitent en ``dépliant'' le trajet de l'onde de manière
à le rendre rectiligne ; on traite alors un problème équivalent
plus simple. Par exemple pour l'onde 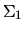 tout se passe comme si la propagation avait eu lieu en ligne droite sur
une distance
tout se passe comme si la propagation avait eu lieu en ligne droite sur
une distance 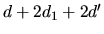 .
On se ramène alors au problème équivalent plus simple
suivant :
.
On se ramène alors au problème équivalent plus simple
suivant :
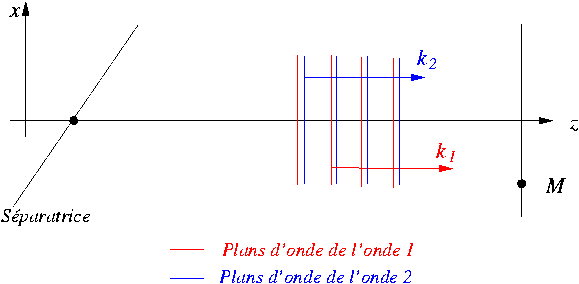
Intensité de l'onde au
point 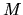
En un point 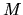 de coordonnées
de coordonnées 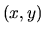 dans le plan d'observation, les amplitudes des deux ondes s'écrivent
dans le plan d'observation, les amplitudes des deux ondes s'écrivent
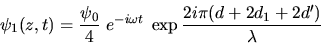
et
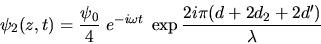
L'intensité s'écrit, en faisant intervenir la quantité 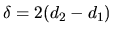 (différence de marche entre les deux ondes
(différence de marche entre les deux ondes 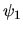 et
et 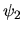 )
:
)
:
![\begin{displaymath}I(z) \; = \; \vert\psi_1+\psi_2\vert^2 \; = \; \frac{\vert\p...... \left[1+ \cos\left(\frac{2 \pi \delta}{\lambda}\right)\right]\end{displaymath}](img71.gif)
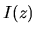 est constante sur tout le plan de l'écran d'observation : on observe
une intensité uniforme dite ``teinte plate''. L'intensité
de cette teinte plate change lorsqu'on fait varier la position du miroir
est constante sur tout le plan de l'écran d'observation : on observe
une intensité uniforme dite ``teinte plate''. L'intensité
de cette teinte plate change lorsqu'on fait varier la position du miroir 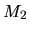 .
Elle décrit la sinusoïde ci-dessous dont la période
est égale à la longueur d'onde (une fraction de micron dans
le visible, ce qui impose des translations de
.
Elle décrit la sinusoïde ci-dessous dont la période
est égale à la longueur d'onde (une fraction de micron dans
le visible, ce qui impose des translations de 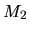 extrèmement faibles pour parcourir la courbe).
extrèmement faibles pour parcourir la courbe).
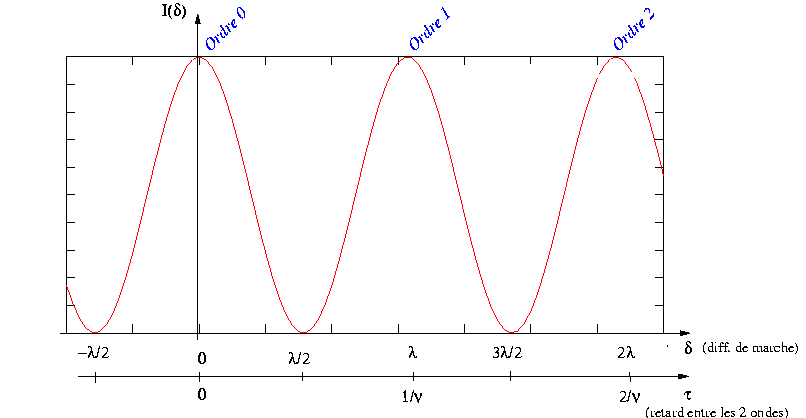
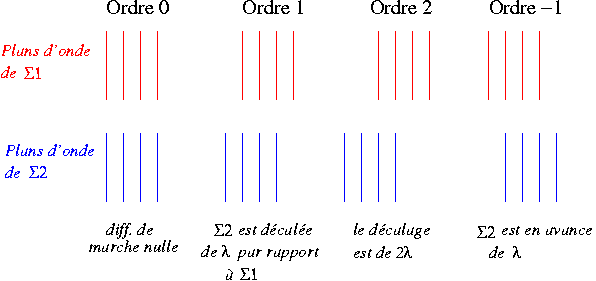
L'ordre d'interférence
Il est défini comme le rapport de la différence de marche
à la longueur d'onde. Il chiffre le nombre de longueurs d'onde que
l'on peut mettre dans la différence de marche. S'il est entier l'interférence
des deux ondes 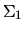 et
et 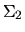 est constructive. S'il est demi-entier, on observera une teinte plate d'intensité
nulle.
est constructive. S'il est demi-entier, on observera une teinte plate d'intensité
nulle.
Remarque
Si 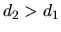 l'onde
l'onde 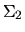 parcourt plus de chemin que l'onde
parcourt plus de chemin que l'onde 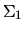 : elle arrive en
: elle arrive en 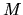 avec un retard
avec un retard 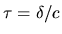 (
(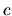 est la vitesse de la lumière). Comme
est la vitesse de la lumière). Comme 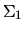 et
et 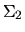 sont deux répliques identiques de l'onde incidente
sont deux répliques identiques de l'onde incidente 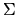 ,
nous avons pratiquement réalisé une interférence entre
l'onde
,
nous avons pratiquement réalisé une interférence entre
l'onde 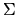 prise au point
prise au point 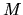 et à l'instant
et à l'instant 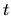 avec la même onde prise au point
avec la même onde prise au point 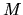 et à l'instant
et à l'instant 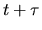 .
Cette notion d'interférence entre une onde et elle-même prise
à un instant différent permet de réaliser l'étude
de la cohérence temporelle des ondes non monochromatiques.
Elle possède de nombreuses applications dans le domaine de la mesure
de largeur et de profil des raies d'émission des gaz excités.
.
Cette notion d'interférence entre une onde et elle-même prise
à un instant différent permet de réaliser l'étude
de la cohérence temporelle des ondes non monochromatiques.
Elle possède de nombreuses applications dans le domaine de la mesure
de largeur et de profil des raies d'émission des gaz excités.
Suivant : Trous
d'Young Précédent : Interférence
d'une onde plane avec elle-même

![]() .
Une partie de l'onde est réfléchie (ici 50% de l'amplitude)
vers un miroir
.
Une partie de l'onde est réfléchie (ici 50% de l'amplitude)
vers un miroir ![]() ,
puis revient vers la séparatrice et la traverse (à nouveau
une perte de 50% de l'amplitude). L'autre partie de l'onde incidente est
transmise vers le miroir réglable
,
puis revient vers la séparatrice et la traverse (à nouveau
une perte de 50% de l'amplitude). L'autre partie de l'onde incidente est
transmise vers le miroir réglable ![]() ,
revient vers la séparatrice et se réfléchit en partie
vers l'écran d'observation. Dans cet exemple on observe une intensité
uniforme (teinte plate).
,
revient vers la séparatrice et se réfléchit en partie
vers l'écran d'observation. Dans cet exemple on observe une intensité
uniforme (teinte plate).

![]() (différence de marche entre les deux ondes
(différence de marche entre les deux ondes ![]() et
et ![]() )
:
)
:
![]() est constante sur tout le plan de l'écran d'observation : on observe
une intensité uniforme dite ``teinte plate''. L'intensité
de cette teinte plate change lorsqu'on fait varier la position du miroir
est constante sur tout le plan de l'écran d'observation : on observe
une intensité uniforme dite ``teinte plate''. L'intensité
de cette teinte plate change lorsqu'on fait varier la position du miroir ![]() .
Elle décrit la sinusoïde ci-dessous dont la période
est égale à la longueur d'onde (une fraction de micron dans
le visible, ce qui impose des translations de
.
Elle décrit la sinusoïde ci-dessous dont la période
est égale à la longueur d'onde (une fraction de micron dans
le visible, ce qui impose des translations de ![]() extrèmement faibles pour parcourir la courbe).
extrèmement faibles pour parcourir la courbe).

