Trous d'Young

C'est un interféromètre à division de front d'onde. Il s'agit d'un écran percé de deux trous minuscules généralement déparés d'une fraction de millimètre pour les expériences en lumière visible. L'ensemble est éclairé par une onde généralement plane (lumière laser) que nous prendrons ici sous incidence normale. Le schéma est le suivant :

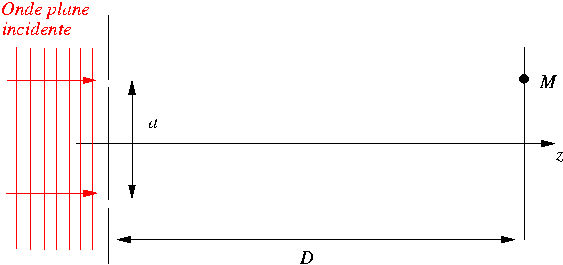
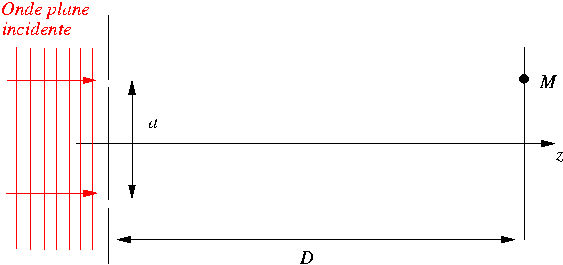
L'onde incidente s'écrit $\psi(z)=\psi_0 \; e^{-i \omega t} \; e^{i k z}$. Dans le plan des trous pris comme origine des $z$, elle vaut simplement $\psi_0 \; e^{-i \omega t}$.

Le coefficient de transmission du masque composé des deux trous peut s'écrire comme la somme de deux petites portes bidimensionnelles identiques de largeur $\epsilon\ll a$ dans les deux directions $x$ et $y$ :
 

$$t(x,y)=\Pi\left(\frac{x-\frac{a}{2}}{\epsilon}\right)\Pi\lef......frac{a}{2}}{\epsilon}\right)\Pi\left(\frac{y}{\epsilon}\right)$$

Ce qui, en utilisant la propriété

$$\lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon}\, \Pi(\frac{x}{\epsilon}) \; = \; \delta(x)$$

peut se modéliser par deux distributions de Dirac bidimensionnelles

$$t(x,y)=\epsilon^2 \left[ \delta\left(x-\frac{a}{2}\right) + \delta\left(x+\frac{a}{2}\right)\right]\; \delta(y)$$

L'application du principe de Huyghens-Fresnel (voir paragraphe XXX) permet alors d'érire l'onde sortant des trous comme la somme de deux ondes sphériques d'amplitudes :
 

$$\psi_1(r,t)=\frac{\psi_{0s}}{r_1} \; e^{-i \omega t} \; e^{i k r_1}$$

$$\psi_2(r,t)=\frac{\psi_{0s}}{r_2} \; e^{-i \omega t} \; e^{i k r_2}$$

avec $\psi_{0s}=\frac{\epsilon^2\; \psi_0}{i \lambda}$ et $r_1$ (resp. $r_2$) désignant la distance entre le trou 1 (resp. 2) et le point courant. On est alors ramené au problème de l'interférence de deux ondes sphériques étudié dans l'introduction de ce chapitre (LIEN). La constante $\psi_{0s}$ est simplement proportionnelle à l'amplitude incidente $\psi_0$ et à la surface du trou $\epsilon^2$.

Lorsque la distance $D$ est grande devant la séparation $a$ des trous, et si on se place près du centre du champ d'interférences, l'onde sphérique peut être assimilée à une onde plane en effectuant le développement limité au premier ordre en $x/D$ et $y/D$ :

$$r_1\; =\; \sqrt{(x-\frac{a}{2})^2+y^2+D^2} \; \simeq \; D+\frac{a^2}{4 D}-\frac{a x}{2 D}$$

$$r_2\; =\; \sqrt{(x+\frac{a}{2})^2+y^2+D^2} \; \simeq \; D+\frac{a^2}{4 D}+\frac{a x}{2 D}$$

d'où
 

$$\psi_1(r,t)\simeq\frac{\psi_{0s}}{D} \; e^{i k \frac{a^2}{4 D}} \; e^{-i \omega t} \; e^{i k (D-\frac{a x}{2 D})}$$

$$\psi_1(r,t)\simeq\frac{\psi_{0s}}{D} \; e^{i k \frac{a^2}{4 D}} \; e^{-i \omega t} \; e^{i k (D-\frac{a x}{2 D})}$$

On est en présence de l'interférence de deux ondes planes dont les cosinus directeurs (projections de $\hat{k}$ sur l'axe $Ox$) sont $\alpha_1=\frac{a}{2D}$ et $\alpha_2=-\frac{a}{2D}$. L'intensité au point $M$ de coordonnées $(x,y)$ dans le champ d'interférences a été écrite dans le paragraphe 1 :

$$I(x)=\mbox{Cte} \; \cos^2 \frac{\pi a x}{\lambda D}$$

On observe des franges de contraste 1 et d'interfrange $i=\lambda D/a$. Ces franges résultent de l'interférence de deux points du même front d'onde de l'onde incidente. Les interférences existent quelle que soit la distance $a$ entre les deux trous, même s'ils sont distants de plusieurs kilomètres : c'est une conséquence du fait que tous les points du front d'onde sont en phase. Cette propriété s'appelle la cohérence spatiale de l'onde. Il existe des ondes qui ne sont pas parfaitement spatialement cohérentes, par exemple les ondes provenant de sources larges (une lampe, le Soleil...). L'étude des interférences produites par ce type d'onde permet d'obtenir des informations sur leur source ; les applications sont nombreuses notamment en astrophysique (mesures des premiers diamètres angulaires d'étoiles dans les années 1920).

Suivant : Cohérence mutuelle  Précédent : Interféromètre de Michelson