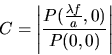Dans l'espace de Fourier la relation 10 devient
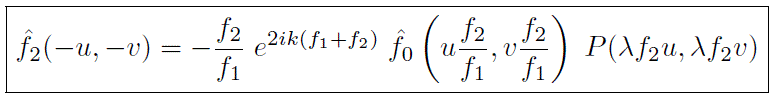 |
(11) |
et fait apparaitre la fonction de transfert du filtrage,
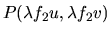 qui n'est autre que la fonction décrivant le coefficient de tranfmission du masque, agrandie d'un facteur
qui n'est autre que la fonction décrivant le coefficient de tranfmission du masque, agrandie d'un facteur
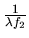 .
Le signe - dans les arguments de
.
Le signe - dans les arguments de 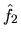 traduit le renversement de l'image.
traduit le renversement de l'image.
Un cas particulier intéressant est celui du montage dit ``4f'' dans lequel les deux lentilles sont identiques f1=f2=f. Les relations objet-image entre les amplitudes deviennent
et dans l'espace de Fourier
l'objet et l'image ont ici la même taille.
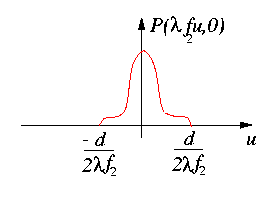 Le masque de filtrage est toujours limité spatialement, souvent il s'agit d'une fente ou d'un trou. La fonction
P(x1,y1) est alors à support borné. Faisons l'hypothèse que P est une fonction paire (comme sur le beau dessin ci-contre) et plaçons-nous sur l'axe y1=0, la fonction
P1(x1,0) s'annule pour
Le masque de filtrage est toujours limité spatialement, souvent il s'agit d'une fente ou d'un trou. La fonction
P(x1,y1) est alors à support borné. Faisons l'hypothèse que P est une fonction paire (comme sur le beau dessin ci-contre) et plaçons-nous sur l'axe y1=0, la fonction
P1(x1,0) s'annule pour
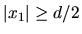 ,
le support est de largeur d. La fonction de transfert du filtrage
,
le support est de largeur d. La fonction de transfert du filtrage
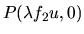 s'annule alors pour une valeur uc dite fréquence de coupure et qui vaut
s'annule alors pour une valeur uc dite fréquence de coupure et qui vaut
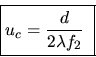 |
(12) |
Physiquement cette valeur représente la fréquence de la sinusoïde la plus serrée que le montage optique est capable d'imager avec un contraste non nul.
En effet considérons un objet sinusoïdal
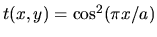 .
Les fréquences spatiales présentes dans cet objet sont 0 et
.
Les fréquences spatiales présentes dans cet objet sont 0 et 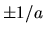 .
Effectuons un filtrage optique de cet objet à l'aide d'un montage 4f. La relation 11 devient, K étant la constante multiplicative
.
Effectuons un filtrage optique de cet objet à l'aide d'un montage 4f. La relation 11 devient, K étant la constante multiplicative
ce qui s'écrit aussi
si la fréquence de la sinusoïde
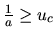 ,
alors
,
alors
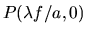 et
et
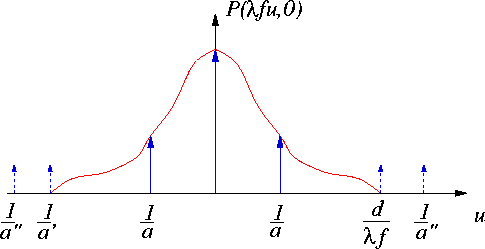
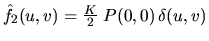 est limitée à son seul pic central. L'image dans le plan P2 est alors uniforme (contraste nul). On dit que le masque P ne transmet pas les fréquences supérieures à uc. La figure ci-dessous illustre ce principe.
est limitée à son seul pic central. L'image dans le plan P2 est alors uniforme (contraste nul). On dit que le masque P ne transmet pas les fréquences supérieures à uc. La figure ci-dessous illustre ce principe.
La fonction de transfert donne une idée du contraste de l'amplitude de l'image dans le plan P2. Cette amplitude s'écrit comme la transformée de Fourier inverse de l'équation précédente
Elle correspond à une sinusoïde de contraste
Ce qui donne une signification physique à la fonction de transfert et une manière de la masurer. La mesure de la fonction de transfert est un moyen de caractériser la qualité des optiques.
En fait l'oeil et les détecteurs sont sensibles à l'intensité et pas à l'amplitude. Pour cette raison la fonction de transfert mesurée est plutôt celle qui correspond à la relation objet-image en éclairage incohérent (relation sur les intensités et non sur les amplitudes).
Figure: Illustration du principe de filtrage d'une mire sinusoïdale. En trait continu : graphe de la fonction de transfert
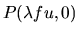 de fréquence de coupure
de fréquence de coupure
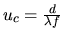 .
Une grille de période a possède les trois fréquences spatiales 0 et
.
Une grille de période a possède les trois fréquences spatiales 0 et
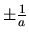 ,
représentées par des pics de Dirac sur le graphe, pour trois grilles de pas a, a', et a" dans le cas oł
,
représentées par des pics de Dirac sur le graphe, pour trois grilles de pas a, a', et a" dans le cas oł
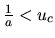 ,
,
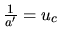 et
et
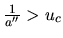 .
Dans le premier cas, les pics latéraux sont multipliés par la constante
.
Dans le premier cas, les pics latéraux sont multipliés par la constante
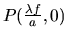 et l'objet filtré correspondant est une sinusoïde de contraste moindre. Dans les deux autres cas, seule la fréquence 0 est transmise, l'image dans le plan P2 est uniforme. Les images du bas donnent l'aspect visuel des trois mires de pas a, a', et a" avant et après filtrage.
et l'objet filtré correspondant est une sinusoïde de contraste moindre. Dans les deux autres cas, seule la fréquence 0 est transmise, l'image dans le plan P2 est uniforme. Les images du bas donnent l'aspect visuel des trois mires de pas a, a', et a" avant et après filtrage.
| Pas | Aspect de la mire | Aspect après filtrage |
| a |  |  |
| a' |  |  |
| a" |  |  |
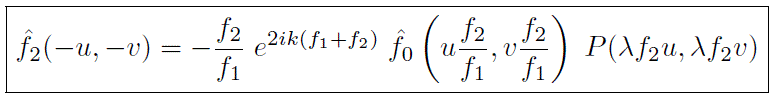
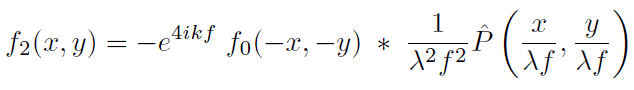
 Le masque de filtrage est toujours limité spatialement, souvent il s'agit d'une fente ou d'un trou. La fonction
P(x1,y1) est alors à support borné. Faisons l'hypothèse que P est une fonction paire (comme sur le beau dessin ci-contre) et plaçons-nous sur l'axe y1=0, la fonction
P1(x1,0) s'annule pour
Le masque de filtrage est toujours limité spatialement, souvent il s'agit d'une fente ou d'un trou. La fonction
P(x1,y1) est alors à support borné. Faisons l'hypothèse que P est une fonction paire (comme sur le beau dessin ci-contre) et plaçons-nous sur l'axe y1=0, la fonction
P1(x1,0) s'annule pour
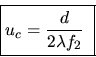
![]() .
Les fréquences spatiales présentes dans cet objet sont 0 et
.
Les fréquences spatiales présentes dans cet objet sont 0 et ![]() .
Effectuons un filtrage optique de cet objet à l'aide d'un montage 4f. La relation 11 devient, K étant la constante multiplicative
.
Effectuons un filtrage optique de cet objet à l'aide d'un montage 4f. La relation 11 devient, K étant la constante multiplicative