On s'intéresse à l'exemple du paragraphe précédent, l'objet est une gaussienne tramée d'écart-type 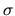 qui s'écrit
qui s'écrit
On désire filtrer cet objet par une fente rectangulaire horizontale de largeur l qui s'écrit
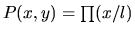 .
L'équation 7 nous permet d'écrire
.
L'équation 7 nous permet d'écrire
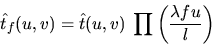 |
(9) |
avec
l'opération de filtrage décrite par l'équation 9 est particulièrement simple à interpréter sur le graphe suivant :
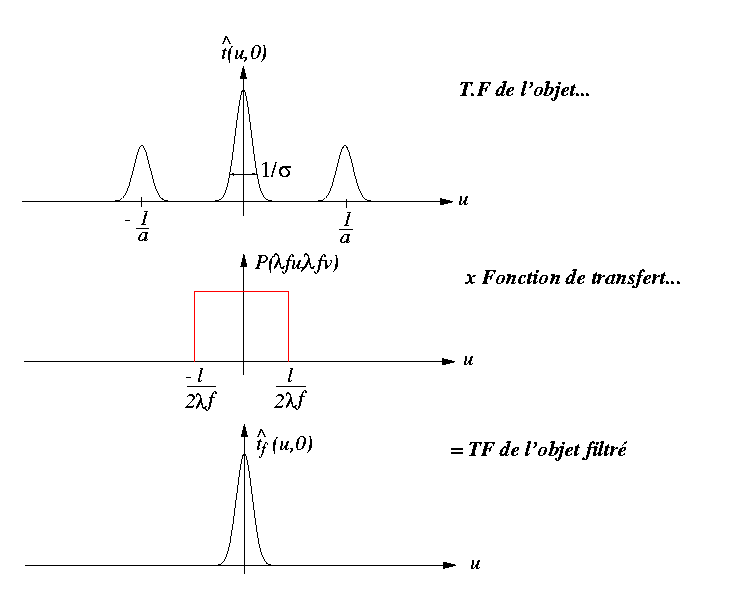
Le filtrage des deux spots latéraux n'est efficace qu'aux conditions suivantes
- Les trois pics sont bien séparés :
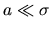
- La taille de la porte est très supérieure à celle du spot central :
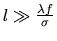
- La porte n'empiète pas sur les lobes secondaires :
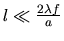
Dans ce cas on peut écrire que la TF de l'objet filtré est égal au pic central :
ce qui permet d'écrire l'objet filtré :
On remarque que la valeur à l'origine de l'objet filtré est moitié de celle de l'objet, ce qui est une expression de la conservation de l'énergie puisque le filtrage a supprimé des fréquences dans la TF de l'objet (application du théorème de Parseval). Ce filtrage a néanmoins permi d'enlever les franges sinusoïdales striant la gaussienne. Un autre exemple de filtrage optique est montré en figure ci-dessous.
Figure 1.1: Application du filtrage optique au détrammage de l'image d'une cellule. Dans la pratique le filtrage ne restitue jamais parfaitement l'image originale (on a coupé une bonne partie des hautes fréquences dans le plan de Fourier). Les détails plus fins que le pas de la trame seront perdus.

![\begin{displaymath}t(x,y)=\exp\left[-\frac{\rho^2}{2\sigma^2}\right]\; \cos^2\left(\frac{\pi x}{a}\right)
\end{displaymath}](img49.gif)
![\begin{displaymath}t(x,y)=\exp\left[-\frac{\rho^2}{2\sigma^2}\right]\; \cos^2\left(\frac{\pi x}{a}\right)
\end{displaymath}](img49.gif)

![\begin{displaymath}t(x,y)=\frac{1}{2}\; \exp\left[-\frac{\rho^2}{2\sigma^2}\right]
\end{displaymath}](img57.gif)
