Dans ce qui suit, nous noterons I(r) la répartition d'intensité au plan focal du télescope. Nous allons décrire de manière très imagée l'évolution des caractéristiques d'une fonction qui est la densité de probabilité du second ordre de l'image aléatoire I(r), lors du processus d'imagerie d'une étoile double tavelée.
Considérons deux positions 
et 
dans l'image. Les intensités qu'on y observe sont respectivement 
et 
. Si 
et 
sont deux valeurs possibles de la fonction d'intensité I(r), la probabilité conjointe dP pour que
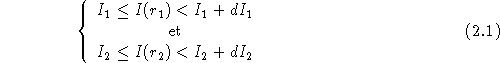
est égale à :
La quantité 
est appelée densité de probabilité du second ordre de la fonction aléatoire I(r).
On suppose souvent dans nos analyses que l'image est invariante par translation ; cette approximation est d'autant plus vérifiée que la turbulence est plus forte et que le champ de speckles s'étend très loin dans l'image. Sous cette hypothèse, la fonction 
ne dépend que du décalage 
. On peut alors écrire :
Et il est évident que
peut être estimé sur un grand nombre d'images comme un histogramme de co-occurence des valeurs en deux points ; ce calcul est illustré en figure 
dans le cas d'un signal monodimensionnel.
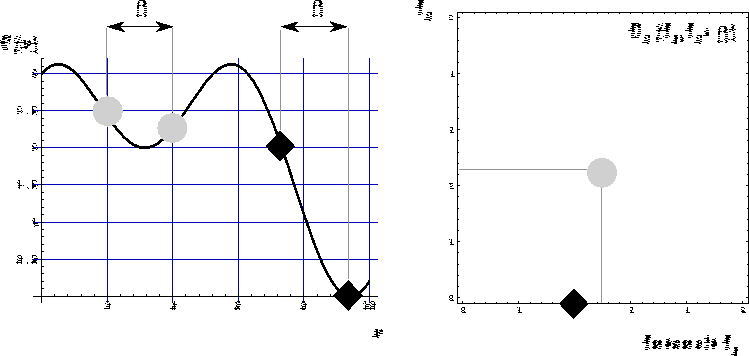
Figure: Illustration du calcul de sur un signal monodimensionnel S(x) (à gauche). Pour un décalage 
donné, on déplace deux points d'analyse sur la courbe S(x) et on porte dans un graphique (à droite) les valeurs et pointées. Dans l'exemple ci-dessus, on pointe 
pour le disque grisé et 
pour le losange noir. Cette opération, répétée sur un grand nombre d'images S(x), fournit une estimation de la densité de probabilité d'ordre deux.
Considérons le cas d'une structure de speckles d'étoile double que nous supposerons orientée sur la direction des abscisses mesurées dans le plan focal. On admet que la condition d'isoplanétisme est vérifiée. On sait que l'image observée est la somme de deux réponses impulsionnelles pondérées par la magnitude des étoiles et décalées d'une quantité égale à la séparation du couple.
Figure: Calcul de la densité de probabilité d'ordre deux pour des tavelures d'étoile double. Sur les images de gauche, on a représenté shématiquement des images de trois tavelures du couple d'étoiles (les deux cercles grisés). Les courbes du milieu représentent des coupes de l'image bidimensionnelle selon une ligne qui passerait au centre d'une tavelure du couple. Les flèches représentent les points d'analyse. A droite, les graphes des densités de probabilité correspondant aux décalages indiqués sur le dessin. Voir le texte pour plus de détails.
Soit 
le rapport d'intensité des étoiles et d leur séparation. Soit s la taille du speckle. Nous prendrons le décalage spatial suivant la direction des abscisses. La figure montre l'evolution des plans 
en fonction du décalage . On observe les phénomènes suivants :
et étant confondus, n'a de valeurs que sur la première diagonale. Elle s'écrit à l'aide de la densité de probabilité du premier ordre P(I) :
peut prendre a priori n'importe quelle valeur, l'excursion de autour de cette valeur est limitée. Ceci se traduit sur le graphe de par une certaine dispersion autour de la première bissectrice, dispersion qui décroît quand le rapport 
augmente.
dûe au nombre élevé d'occurences de sur un speckle de la première étoile et de sur la deuxième. La pente de cette droite est le rapport d'intensité des étoiles.
est complètement rempli. Lorsque les speckles sont contenus dans une enveloppe limitée (ce qui est en général le cas) il arrive que les points d'analyse pour les grands décalages tombent l'un dans la tache image et l'autre dans le fond du ciel. Ceci se traduit par des valeurs anormalement élevées de la densité de probabilité sur les deux axes 
et 
.
On voit sur cet exemple simple comment la simple analyse visuelle des figures des densités de probabilité permet d'accéder au vecteur séparation et à la différence de magnitude entre les étoiles. Pour une image réelle, le décalage s'exprime en unités de pixels et peut prendre 
valeurs si l'image est de dimension 
. On obtient le vecteur séparation en examinant les plans 
pour toutes les valeurs de et en recherchant la présence d'une ligne de crête. La différence de magnitude entre les étoiles est simplement donnée par la pente de la ligne de crête. Il est important de remarquer ici que est déterminé sans équivoque : une valeur mesurée de 0.8 signifie que la deuxième étoile rencontrée lorsqu'on balaye les images pour calculer la densité de probabilité possède une intensité de 0.8 fois celle de la première. L'image du systême peut alors être obtenue sans ambiguité. La même analyse aurait pu être faite sur les fonctions caractéristiques, transformées de Fourier de la densité de probabilité dans les plans 
et qui présente de la même façon une direction privilégiée lorsqu'elle est calculée pour un décalage égal au vecteur séparation.