Considérons un système de trois étoiles, chacune séparée de ses voisines d'une quantité grande devant la taille du speckle. On note 
le rapport d'intensité de la deuxième étoile à la première, 
le rapport de la troisième étoile à la première. On note 
le vecteur séparation entre les étoiles 1 et 2, 
le vecteur séparation entre les étoiles 1 et 3. Les matrices D et R définies aux équations 2.20 et 2.22 de l'article précédent s'écrivent dans ce cas :
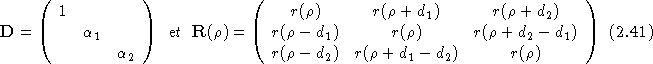
On se place maintenant dans le cas particulier de la figure 
où les trois étoiles sont alignées et équidistantes, soit d cette distance. Les fonctions caractéristiques pour les décalages 
et 
s'expriment alors, en utilisant l'équation 2.25 de l'article :
Pour la fonction caractéristique a la même expression que celle qui serait calculée pour une étoile double de rapport d'intensité et de séparation 2d. Pour elle montre deux axes privilégiés d'équation :
Les modules de ces fonctions sont représentés en figure pour les valeurs 
et 
.
On peut généraliser cette analyse à un système de N étoiles. On note 
les intensités de chaque étoile. On suppose qu'il existe dans le système un nombre K de couples d'étoiles qui ont chacun la même séparation d (redondances), et que les étoiles en correspondance dans chaque couple portent les numéros (p,p+N-K) ; par exemple pour l'étoile triple dont nous venons de parler, les couples distants de d étaient (1,2) et (2,3).
On peut, toujours sous l'hypothèse que d est grand devant la taille du speckle, calculer la taille de la séparation d :
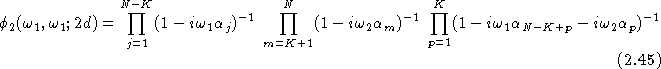
Cette fonction montrerait alors K axes privilégiés d'équation :
Cet exemple simple montre comment la fonction caractéristique d'ordre deux permet d'obtenir, dans le cas de systèmes d'étoiles multiples, les différentes positions et intensités des étoiles. Dans le cas particulier où le système possède des redondances pour une certaine séparation entre ses étoiles, le module de 
montre plusieurs lignes obliques dont les pentes sont reliées de manière très simple aux rapports d'intensité des étoiles des couples redondants. Dans le cas trivial de l'étoile triple dont les composantes sont équidistantes et alignées, l'examen de la fonction caractéristique à deux décalages différents donne sans ambiguité les rapports et .
Figure: Fonction caractéristique au deuxième ordre d'une structure de speckles d'étoile triple bien séparée dont les composantes sont alignées et équidistantes. On a pris et . En (a) on a représenté l'objet. En (b) et (c) les modules des fonctions caractéristiques correspondant à et .