Les variations de phase sur l'onde étant aléatoires, il est impossible de modéliser les champs de tavelures de manière déterministe. On ne peut que décrire leurs propriétés statistiques en considérant que l'onde qui arrive au plan focal du télescope est la somme d'ondes élémentaires et s'écrit :
On peut supposer de manière très générale que
de toutes les ondes élémentaires sont indépendantes, et la phase 
d'une onde élémentaire,
,
.
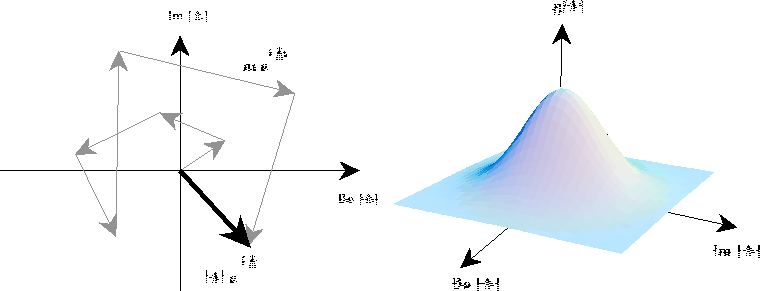
Figure: L'amplitude complexe de l'onde au foyer du télescope est la somme d'un grand nombre d'ondes élémentaires ; le phénomène est assimilable à une marche aléatoire bidimensionnelle (à gauche) conduisant à une densité de probabilité gaussienne pour l'onde résultante (à droite).
Chacune des ondes élémentaires peut être représentée dans le plan complexe par un vecteur de Fresnel (figure 
) et le problème se ramène à celui d'une marche aléatoire bidimensionnelle. Lorsque N devient très grand, on peut appliquer le théorème de la limite centrale et la densité de probabilité de l'amplitude complexe de l'onde résultante prend une forme asymptotique gaussienne indépendante des propriétés du milieu diffuseur [32, 42]
où 
et 
sont les parties réelles et imaginaires de l'amplitude complexe A et 
, sa variance est la demi-somme des variances des ondes :
Un changement de variable simple (c'est un passage en coordonnées polaires) permet d'écrire la densité de probabilité de l'intensité au plan focal, carré du module de l'amplitude complexe :
Cette fonction est indépendante de la position dans l'image et décrit un champ de speckle qui s'étend à l'infini (hypothèse stationnaire). Sa transformée de Fourier est la fonction caractéristique
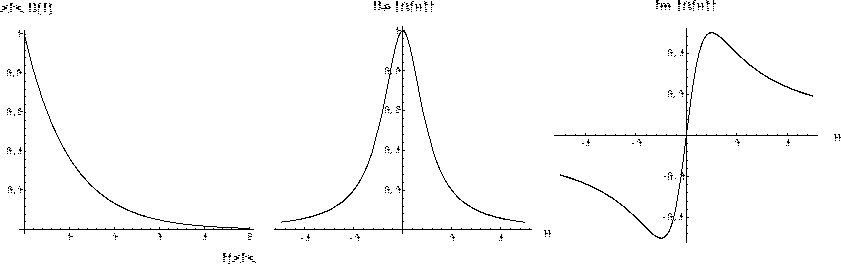
Figure: Densité de probabilité (à gauche) et fonction caractéristique (au milieu, partie réelle, à droite, partie imaginaire) d'une structure de speckles gaussienne pour un point source.
Ce modèle est particulièrement adapté à la description des champs de speckles produits par la diffusion d'une lumière laser dans un milieu inhomogène : ce sont les molécules qui diffusent la lumière et leur nombre est extrèmement élevé. L'hypothèse gaussienne est une bonne approximation en astronomie quand la turbulence est particulièrement mauvaise et/ou quand le diamètre du télescope est grand ; le nombre N d'ondes élémentaires indépendantes qui forment les tavelures observées est de l'ordre de celui des zones de cohérences intersectées par la pupille du télescope, soit 
. Si ce nombre n'est pas assez élevé pour appliquer le théorême de la limite centrale, la statistique des champs de speckles au foyer dépend de celle de l'amplitude complexe sur la pupille (dont on sait qu'elle est plutôt log-normale et présente essentiellement des fluctuations de phase [2, 29]).
