On peut supprimer la première lentille et placer l'objet à grande distance de la lentille restante : on réalise ainsi une vraie diffraction de Fraunhofer entre le plan de l'objet et le plan du masque. Le montage optique est alors le suivant :
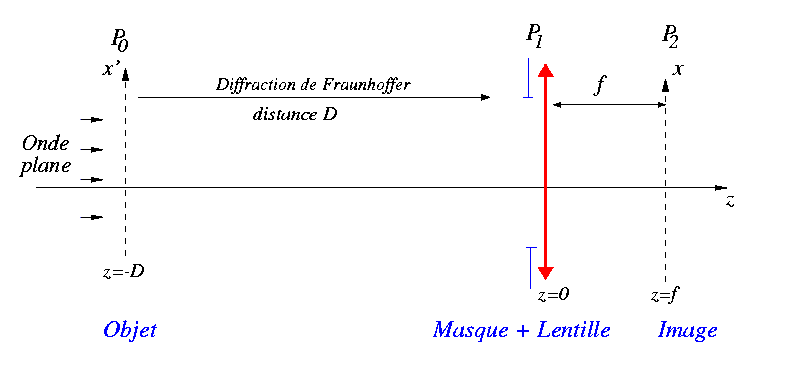
Les notations sont les suivantes
- Amplitude de l'onde incidente dans le plan de l'objet :
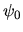
- t(x',y') : coefficient de transmission de l'objet
- Distance objet-masque : D, assez grand pour pouvoir faire l'approximation de Fraunhofer
- Lentille de focale f et masque
P(x1,y1) dans le même plan pris comme origine des z
- f2(x,y) : amplitude au plan focal
A la sortie de l'objet (z=-D), l'amplitude s'écrit
Une première diffraction de Fraunhofer permet d'écrire l'amplitude à l'entrée du masque
puis sur la lentille
On utilise la relation (1) qui donne l'amplitude au foyer de la lentille
 Posons
Posons
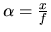 et
et
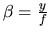 .
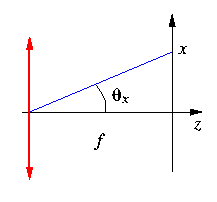
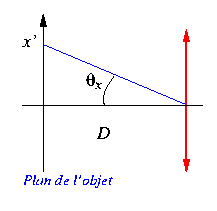
Ce sont les sinus des deux angles
.
Ce sont les sinus des deux angles 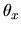 et
et 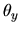 sous lesquel est vu un point du plan focal image (x,y) depuis le centre de la lentille (dessin ci-contre). Posons aussi
sous lesquel est vu un point du plan focal image (x,y) depuis le centre de la lentille (dessin ci-contre). Posons aussi
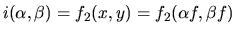 .
Alors que f2(x,y) désigne l'amplitude en un point (x,y) de l'image (répartition spatiale d'amplitude),
.
Alors que f2(x,y) désigne l'amplitude en un point (x,y) de l'image (répartition spatiale d'amplitude),
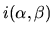 désigne l'amplitude diffractée dans la direction
désigne l'amplitude diffractée dans la direction
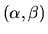 ,
c'est donc une répartition angulaire d'amplitude dans l'image.
,
c'est donc une répartition angulaire d'amplitude dans l'image.
Il vient
 Posons
Posons
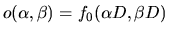 ,
cette fonction désigne l'amplitude observée depuis le centre de la lentille dans une direction
,
cette fonction désigne l'amplitude observée depuis le centre de la lentille dans une direction
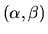 ,
c'est à dire la répartition angulaire d'amplitude sur l'objet. Nous aboutissons à la relation de convolution suivante :
,
c'est à dire la répartition angulaire d'amplitude sur l'objet. Nous aboutissons à la relation de convolution suivante :
Cette relation entre les répartitions angulaires d'amplitude est indépendante de la focale de la lentille et de la distance de l'objet. La réponse impulsionnelle du filtrage est la transformée de Fourier du coefficient de transmission du masque
Cette relation est à comparer à celle qui existe entre les répartitions spatiales d'amplitude entre les plans P0 et P2 d'un montage à double diffraction (eq. (10)). Outre l'indépendance par rapport aux focales, nous avons ici un terme multiplicatif
![$\exp\left[i\pi\lambda f (\alpha^2+\beta^2) \right]$](img114.gif) qui dépend des variables
qui dépend des variables
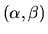 .
.
Cependant ce calcul est fait dans les limites de l'optique paraxiale avec des angles inférieurs à la dizaine de degrés (voir paragraphe correspondant). Dans le visible,
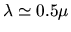 m, les focales moyennes dont de quelques dizaines de centimètres, prenons par exemple f=1 m. Posons
m, les focales moyennes dont de quelques dizaines de centimètres, prenons par exemple f=1 m. Posons
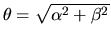 .
Nous sommes en optique paraxiale si
.
Nous sommes en optique paraxiale si
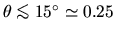 rad. L'argument de l'exponentielle vaut alors
rad. L'argument de l'exponentielle vaut alors
et le facteur multiplicatif
![$\exp\left[i\pi\lambda f (\alpha^2+\beta^2) \right]$](img114.gif) est donc toujours quasiment égal à un en optique paraxiale. On peut donc ré-écrire la relation de convolution objet-image :
est donc toujours quasiment égal à un en optique paraxiale. On peut donc ré-écrire la relation de convolution objet-image :
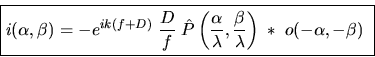 |
(13) |


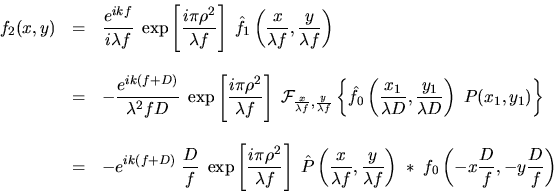
 Posons
Posons
 Posons
Posons
![]() m, les focales moyennes dont de quelques dizaines de centimètres, prenons par exemple f=1 m. Posons
m, les focales moyennes dont de quelques dizaines de centimètres, prenons par exemple f=1 m. Posons
![]() .
Nous sommes en optique paraxiale si
.
Nous sommes en optique paraxiale si
![]() rad. L'argument de l'exponentielle vaut alors
rad. L'argument de l'exponentielle vaut alors