Le ``Speckle Masking'' ou opérateur de Weigelt

Il s'agit d'une analyse qui fait intervenir le moment du troisième ordre des champs de speckles : la triple corrélation ou sa transformée de Fourier, le bispectre. Ce sont des fonctions quadridimensionnelles dépendant l'une de deux décalages spatiaux, l'autre de deux fréquences spatiales.

L'idée sous-jacente à la naissance de cette technique était la suivante [77] : considérons un objet astronomique O(r) présentant une structure telle qu'en le superposant à lui-même décalé d'une certaine quantité 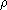on obtienne presque un point (comme dans l'exemple de la figure ). Convoluée par une réponse impulsionnelle tavelée, cette intersection fournit une estimation grossière de cette réponse impulsionnelle : on retrouve le cas le l'holographie des tavelures. Cette idée de superposer les tavelures a valu à cette technique le nom de ``Speckle Masking''.

  
Figure: Illustration de la technique ``Speckle Masking''. A gauche, l'objet astronomique observé présente une morphologie telle qu'en le décalant par rapport à lui-même, la superposition est presque un point. La même opération effectuée sur une image tavelée de l'objet permet une estimation de la réponse impulsionnelle.

Mathématiquement l'opération peut s'écrire de la façon suivante [57]. Si I(r) est l'intensité dans l'image et 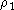le décalage approprié, la réponse impulsionnelle est simplement le produit :

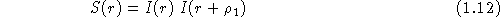
En intercorrélant cette fonction avec toute l'image comme dans le cas de l'holographie, on obtient la quantité

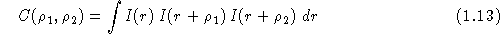
qui est la triple corrélation de l'image et qui contient a priori l'information sur la phase de l'objet. Les relations de convolution entre les corrélations restent vraient pour les triples corrélations, et si on note TC[f] la triple corrélation d'une fonction f on peut écrire :

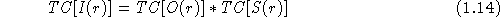
La double transformée de Fourier de cette relation par rapport aux deux variables d'espace donne une multiplication simple des bispectres (notés ) :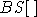

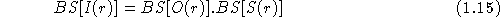
Comme pour l'ordre deux, le bispectre de la réponse impulsionnelle S peut être estimé sur une étoile de référence proche. L'objet est alors restitué à partir de son bispectre ; deux méthodes sont actuellement utilisées.

• Une reconstruction récursive faisant intervenir les relations de clôture entre les points de la phase du bispectre,
• Une méthode de type Monte Carlo où l'on reconstruit l'objet point par point en minimisant une distance entre le bispectre des objets successifs et celui qui est observé.

Là encore, on trouve une description détaillée de ces méthodes dans l'article de revue de Weigelt [78].

Roddier [69] a montré ont montré que la méthode de Knox et Thompson et celle de Labeyrie ne sont que des cas particuliers de l'analyse bispectrale ; elles s'appuient en fait sur des relations de clôture de phase. D'importants travaux théoriques ont été effectués sur ce sujet [19, 53], et des études comparatives de reconstruction d'images par les méthodes Knox-Thompson et Speckle Masking ont été présentées par Beletic [28] au colloque de l'ESO en Octobre 1991.