La fonction d'autocorrélation d'une image S(r) s'écrit :
ou de manière équivalente en faisant intervenir la fonction caractéristique :
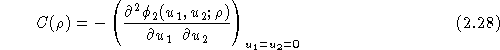
En utilisant les expressions 
ou , l'autocorrélation prend la forme simple :
Sa transformée de Fourier, la fonction de transfert, s'écrit :
La fonction 
est la transformée de Fourier de la densité de probabilité 
par rapport à la variable d'espace 
. L'intérêt de cette fonction sera discuté plus loin pour l'application de l'imagerie probabiliste à la synthèse d'ouverture.
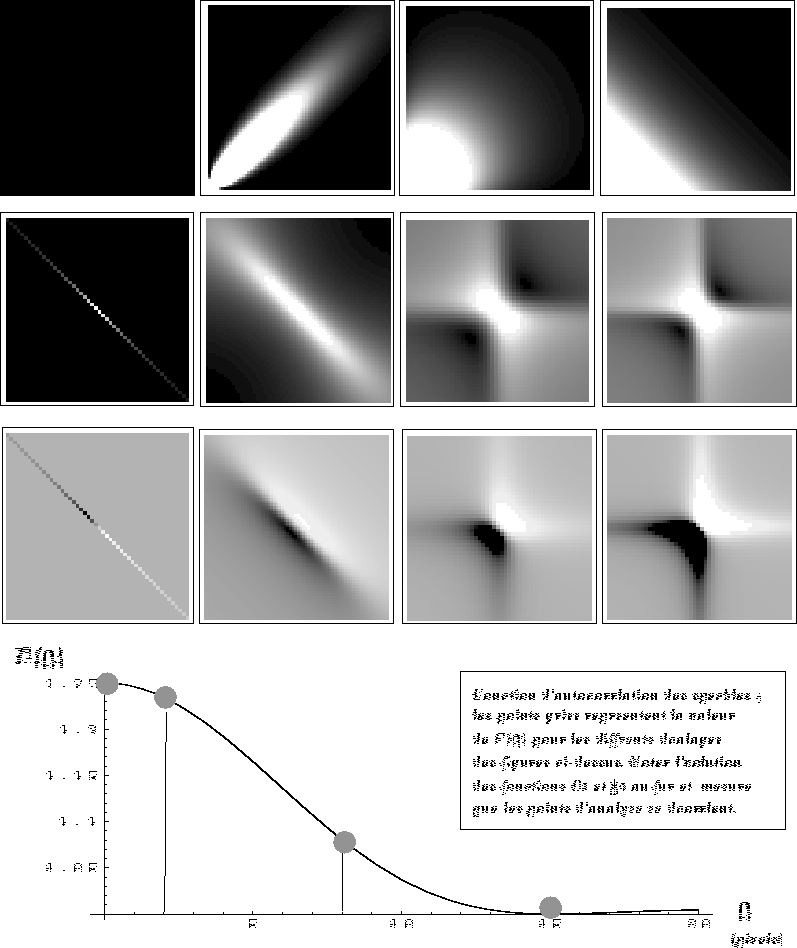
Figure: Visualisation en niveaux de gris de la densité de probabilité d'ordre 2 (au dessus) et de la fonction caractéristique (partie réelle au milieu et partie imaginaire au dessous) d'une structure de speckle gaussienne pour un point source aux décalages 
, 
, 
, 
. Les décalages sont reportés sur la courbe de la fonction de corrélation de l'amplitude complexe comme des petits disques grisés.
