L'image d'une étoile double observée en présence de turbulence est la superposition de deux structures tavelées décalées d'une quantité égale à la séparation du couple (d) et pondérées par le rapport d'éclat entre les étoiles ( 
). Si la condition d'isoplanétisme est vérifiée, l'image I(r) observée est :
L'intensité observée est la somme de deux variables aléatoires qui sont décorrélées si la séparation du couple est grande devant la taille du speckle. On peut ainsi écrire :
où 
est la contribution à l'intensité I du champ de tavelures de la première étoile, et 
celle de la deuxième étoile. et sont deux variables aléatoires qui obéissent chacune à la loi exponentielle décroissante définie au paragraphe précédent :
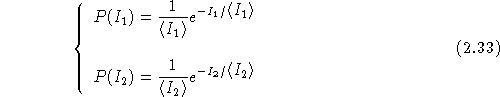
avec 
. La densité de probabilité s'écrit dans ce cas [32] :
Il est intéressant de remarquer que cette fonction est très différente de la densité de probabilité de la réponse impulsionnelle donnée par l'équation 
; elle s'annule pour I=0 et présente un maximum à la valeur
Cette valeur peut être utilisée pour déterminer le rapport d'intensité entre les deux composantes du système double, la densité de probabilité du premier ordre pouvant être estimée sur un ensemble d'images comme un histogramme des valeurs des pixels. Une détermination du maximum de cet histogramme permet (dans les limites où le modèle Gaussien est applicable) d'obtenir une estimation de la valeur du rapport . La simple inspection visuelle de l'histogramme peut diagnostiquer la duplicité du systême. Par contre, aucune information spatiale sur l'étoile double ne peut être obtenue de cette manière. Il faut pousser l'analyse au second ordre pour connaitre le vecteur séparation du couple.
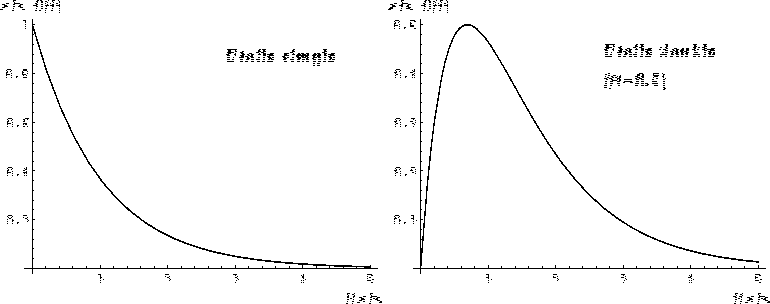
Figure: Densités de probabilité de champs de speckles gaussiens. A gauche, pour un point source, à droite pour une étoile double de rapport d'intensité 
.
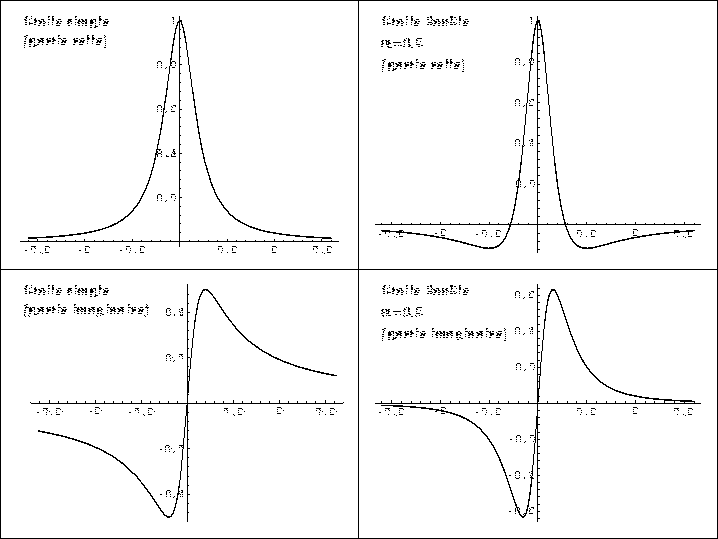
Figure: Fonctions caractéristiques correspondantes.
La fonction caractéristique est la transformée de Fourier de l'expression :
C'est une fonction dont la partie réelle présente des ``pieds'' négatifs qui n'étaient pas observés dans le cas de l'étoile simple (voir la figure ). La différence avec la réponse impulsionnelle n'est cependant pas aussi spectaculaire que pour la densité de probabilité.
