Le recuit simulé est une technique de type Monte-Carlo généralisé très à la mode actuellement en traitement d'images. C'est une méthode de minimisation d'une fonctionnelle (qui peut être une distance entre une observation et un modêle) qui a la propriété de converger vers le minimum global de la fonction s'il existe (refs).
Nous allons décrire la procédure de reconstruction d'un objet O(r) digitalisé sur N points par minimisation d'une distance entre les fonctions caractéristiques du modèle et observée, à l'ordre deux. Soient 
et 
les intensités et les positions des points de l'objet.
Si on utilise le modèle gaussien, la fonction caractéristique du modèle s'exprime [9]:
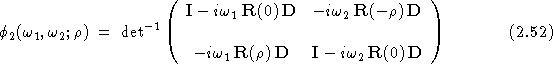
où les notations sont celles de l'article, soit 
la covariance de l'amplitude complexe de l'onde, 
la matrice diagonale des intensités dans l'objet et 
la matrice unité.
Si on utilise la modèle avec étoile de référence, la fonction caractéristique est :
La procédure de reconstruction est la même que l'on utilise l'un ou l'autre de ces modêles. Soit 
la fonction caractéristique calculée par le modèle et 
celle qui est mesurée sur les données. On va ajuster les paramètres et de telle sorte que la distance :
soit minimale. L'algorithme utilise la technique de recuit simulé, il est décrit par l'organigramme de la figure 
.
Figure: Algorithme de recuit simulé proposé pour la minimisation des distances entres fonctions caractéristiques du deuxième ordre d'un modèle et d'une observation (reproduction d'une partie du poster présenté au colloque de l'ESO en Octobre 1991 (voir annexe 2).
Le choix de la fonction distance W (on dit aussi fonction de coût) est arbitraire et dépend du problème physique auquel on s'intéresse. Il peut s'agir de la norme euclidienne, c'est à dire la somme des carrés des différences point par point des deux fonctions caractéristiques :
Il peut aussi s'agir de la distance entre des fonctions qui dépendent des 
comme le logarithme de ou pondérée par une certaine quantité. On peut également minimiser la différence entre les densités de probabilité. Le tout est d'utiliser une fonctionnelle qui soit physiquement acceptable et qui conduise à un minimum global le plus marqué possible. Des études sont actuellement en cours sur des simulations de tavelures d'étoiles doubles, elles sont présentées dans le paragraphe .
On introduit parfois en addition à la fonction de coût une fonction dite de pénalité pour tenir compte d'éventuelles contraintes physiques sur l'objet . La fonctionnelle à minimiser devient alors :
La fonction de pénalité peut être la dérivée ou la dérivée seconde de l'objet (critère de lissage). On peut aussi introduire une limitation spatiale de l'étendue de l'objet (contrainte de support), etc... Le coefficient 
est le paramètre de régularisation.
